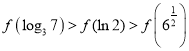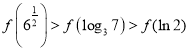题目内容
【题目】下列说法:
①若集合![]() ,
,![]() ,则
,则![]() ;
;
②定义在![]() 上的函数
上的函数![]() , 若
, 若![]() 为奇函数,则必有
为奇函数,则必有![]() ;
;
③方程![]() 有两个实根;
有两个实根;
④存在![]() ,
,![]() ,使得
,使得![]() .
.
其中说法正确的序号是( )
A.②③B.②④
C.①②③D.②
【答案】B
【解析】
求出集合![]() 、
、![]() ,根据集合的包含关系可判断命题①的正误;根据奇函数的定义可判断出命题②的正误;作出函数
,根据集合的包含关系可判断命题①的正误;根据奇函数的定义可判断出命题②的正误;作出函数![]() 和函数
和函数![]() 的图象,观察两函数图象的交点个数,可判断出命题③的正误;取特殊值可判断出命题④的正误.
的图象,观察两函数图象的交点个数,可判断出命题③的正误;取特殊值可判断出命题④的正误.
对于命题①,![]() ,
,![]() ,则
,则![]() ,命题①错误;
,命题①错误;
对于命题②,已知函数![]() 是定义在
是定义在![]() 上的奇函数,则
上的奇函数,则![]() ,即
,即![]() ,解得
,解得![]() ,命题②正确;
,命题②正确;
对于命题③,作出函数![]() 和函数
和函数![]() 的图象如下图所示:
的图象如下图所示:
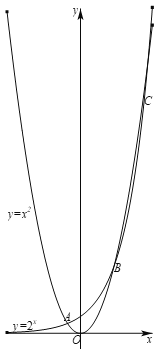
由图象可知,两个函数的图象有三个交点,则方程![]() 有三个实根,命题③错误;
有三个实根,命题③错误;
④取![]() ,
,![]() ,则
,则![]() ,
,![]() ,命题④正确.
,命题④正确.
综上,正确命题的序号为②④.
故选:B.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
以这100台机器维修次数的频率代替1台机器维修次数发生的概率, 记![]() 表示1台机器三年内共需维修的次数,
表示1台机器三年内共需维修的次数,![]() 表示购买1台机器的同时购买的维修次数.
表示购买1台机器的同时购买的维修次数.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以在维修上所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?