题目内容
15.已知A(3,0),B(0,3)C(cosα,sinα).(1)若$\overrightarrow{AC}$•$\overrightarrow{BC}$=-1,求sin(α+$\frac{π}{4}$)的值;
(2)若|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{13}$,且α∈(0,π),求$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角.
分析 (1)由题意利用两个向量的数量积公式可得 $\overrightarrow{AC}•\overrightarrow{BC}$=1-3(sinα+cosα)=-1,求得sinα+cosα=$\frac{2}{3}$,可得sin(α+$\frac{π}{4}$)的值.
(2)求出 $\overrightarrow{OA}$+$\overrightarrow{OC}$=(3+cosα,sinα),则由题意可得 $\sqrt{{(3+cosα)}^{2}{+sin}^{2}α}$=$\sqrt{13}$,化简求得cosα 的值,可得α 的值.设$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为θ,由cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}|•|\overrightarrow{OC}|}$ 的值,求得θ的值.
解答 解:(1)由题意可得 $\overrightarrow{AC}$=(cosα-3,sinα),$\overrightarrow{BC}$=(cosα,sinα-3),
∴$\overrightarrow{AC}•\overrightarrow{BC}$=(cosα-3,sinα)•(cosα,sinα-3)=cosα(cosα-3)+sinα(sinα-3)=1-3(sinα+cosα)=-1,
∴sinα+cosα=$\frac{2}{3}$,即 $\sqrt{2}$sin(α+$\frac{π}{4}$)=$\frac{2}{3}$,求得sin(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{3}$.
(2)∵$\overrightarrow{OA}$+$\overrightarrow{OC}$=(3+cosα,sinα),若|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{13}$,且α∈(0,π),
则有 $\sqrt{{(3+cosα)}^{2}{+sin}^{2}α}$=$\sqrt{13}$,化简求得cosα=$\frac{1}{2}$,∴α=$\frac{π}{3}$.
设$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为θ,cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}|•|\overrightarrow{OC}|}$=$\frac{3sinα}{3×1}$=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,∴θ=$\frac{π}{6}$,
即$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为$\frac{π}{6}$.
点评 本题主要考查两个向量的数量积公式,求向量的模,属于基础题.

| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
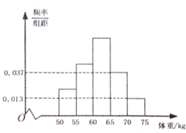 为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )
为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
| A. | cos(2x-1) | B. | -2cos(2x-1) | C. | 2cos(2x-1) | D. | -cos(2x-1) |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
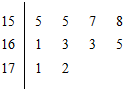 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.