题目内容

4．函数y=2sinx，x∈[0，2π]与y=$\frac{3}{2}$的交点个数为（　　）
A．0B．1C．2D．3

分析 作出两个函数的图象，利用数形结合进行求解即可．

解答 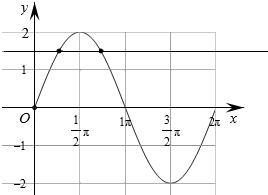解：∵x∈[0，2π]，
∴作出y=2sinx在x∈[0，2π]上以及y=$\frac{3}{2}$的图象，
由图象知，两个图象的交点为2个，
故选：C．

点评 本题主要考查函数交点个数的判断，利用数形结合是解决本题的关键，比较基础．

练习册系列答案
相关题目
14．已知命题：①“所有能被3整除的整数都是奇数”的否定是“存在一个能被3整除的整数不是奇数”
②“菱形的两条对角线互相垂直”的逆命题；
③“a，b，c∈R，若a＞b，则a+c＞b+c”的逆否命题；
④“若a+b≠3，则a≠1或b≠2”．上述命题中真命题的个数为（　　）
A．1B．2C．3D．4
15．已知A（3，0），B（0，3）C（cosα，sinα）．
（1）若$\overrightarrow{AC}$•$\overrightarrow{BC}$=-1，求sin（α+$\frac{π}{4}$）的值；
（2）若|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{13}$，且α∈（0，π），求$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角．
12．已知t（单位：秒）时间与S（单位：米）路程之间的关系是：S（t）=3t2+1，则在t=2秒时的瞬时速度是12m/s．
19．直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为（　　）
A．4$\sqrt{2}$B．4C．2$\sqrt{2}$D．2
5．某程序框图如图所示，若该程序运行后输出的值是$\frac{5}{6}$，则（　　）
A．a=4B．a=5C．a=6D．a=7
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线与圆x2+y2-4x+2=0，有公共点，则该双曲线离心率的取值范围是（　　）
A．（1，2]B．[$\sqrt{2}$，+∞）C．（1，$\sqrt{2}$]D．（1，$\sqrt{2}$）
9．用分析法证明$\sqrt{3}+\sqrt{5}$＞$\sqrt{2}+\sqrt{4}$．
10．两直线（2m-1）x+y-3=0与6x+my+1=0垂直，则m的值为（　　）
A．0B．$\frac{6}{11}$C．$\frac{6}{13}$D．0或$\frac{6}{13}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网