题目内容
【题目】已知在正整数n的各位数字中,共含有![]() 个1,
个1,![]() 个2,,
个2,,![]() 个n.证明:
个n.证明:![]() 并确定使等号成立的条件.
并确定使等号成立的条件.
【答案】见解析
【解析】
对正整数n的位数使用数学归纳法.
当![]() 是一位数,即
是一位数,即![]() 时,所证式显然成立,
时,所证式显然成立,
这是因为,此时![]() 的十进制表达式中只有一位数字
的十进制表达式中只有一位数字![]() ,
,
即![]() ,其余
,其余![]() ,所以,左边=
,所以,左边=![]() =右边.
=右边.
假设当正整数![]() 不超过k位,即
不超过k位,即![]() 时,结论皆成立.
时,结论皆成立.
现考虑![]() 为
为![]() 位数,即
位数,即![]() 时的情形.
时的情形.
设![]() 的首位数字为r.则
的首位数字为r.则![]() . ①
. ①
若![]() ,则在数
,则在数![]() 的各位数字中,
的各位数字中,![]() ,其余
,其余![]() .
.
显然,![]() .
.
若![]() ,记
,记![]() 的各位数字中含有
的各位数字中含有![]() 个1,
个1,![]() 个2,…,
个2,…,![]() 个r,…,
个r,…,![]() 个9.
个9.
则![]() 的各位数字中,含有
的各位数字中,含有![]() 个r、
个r、![]() 个j
个j![]() .
.
注意到,正整数![]() 不超过k位.
不超过k位.
由归纳法假设,对![]() 有
有
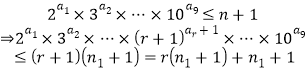
![]() ②
②
则当![]() 为
为![]() 位数时,结论也成立.
位数时,结论也成立.
故由数学归纳法,知对一切正整数![]() ,结论皆成立.
,结论皆成立.
欲使等号成立,由证明过程,知要么![]() 为一位数;要么在
为一位数;要么在![]() 的位数大于或等于2时,由式②,必须
的位数大于或等于2时,由式②,必须![]() ,此时,由式①得
,此时,由式①得![]() ,
,
即![]() 可表示为
可表示为![]() 的形式.
的形式.
上述条件也是充分的,当![]() 能够表成以上形式时,有
能够表成以上形式时,有![]() ,其余
,其余![]() .
.
故![]()

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目