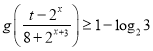Question

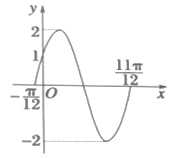
【题目】已知函数，（，，）的部分图像如图所示.

（1）求函数的解析式及图像的对称轴方程；

（2）把函数图像上点的横坐标扩大到原来的2倍（纵坐标不变），再向左平移个单位，得到函数的图象，求关于x的方程在时所有的实数根之和.

Answer 1

【答案】（1），（）；（2）

【解析】

（1）根据图像的最小正周期、最值和过点可分别确定、、，即可得到函数表达式；令，即可求出对称轴；

（2）根据题意先求出，再利用三角函数的对称性即可求解.

（1）由题设图象知，最小正周期，，

最大值为，，

点在函数图象上，即，

又 ，，从而.

故函数的解析式为.

令，，解得，即为函数图像的对称轴方程.

（2）依题意，得，

的周期，

在内有2个周期.

令，所以，

即函数的对称轴为.

又，则且，

所以在内有4个实根.

不妨从小到大依次设为，

则，.

∴关于的方程在时所有的实数根之和为.