题目内容
【题目】抛物线![]() 的焦点是
的焦点是![]() .问:是否存在内接等腰直角三角形,该三角形的一条直角边过
.问:是否存在内接等腰直角三角形,该三角形的一条直角边过![]() 点?如果存在,存在几个?如果不存在,说明理由.
点?如果存在,存在几个?如果不存在,说明理由.
【答案】见解析
【解析】
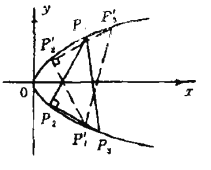
如图,设一条直角边是![]() ,则直线
,则直线![]() 的方程是
的方程是![]() .
.
由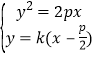
得到![]() .
.
其判别式为![]()
![]() .
.
可见,![]() ,
,![]() 两点的横坐标
两点的横坐标![]() ,
,![]() 与纵坐标
与纵坐标![]() ,
,![]() ,分别是
,分别是
![]() ,
,![]() .
.
考虑复平面,设向量![]() ,
,
于是,![]()
![]() .
.
从而,![]()
![]()
![]() .
.
注意到![]() 在
在![]() 上,
上,
因此![]() .
.
整理得 ![]() . ①
. ①
将①两边平方,整理得![]() . ②
. ②
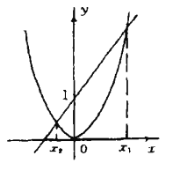
做出函数![]() 和
和![]() 的图象,可以看出这两个图象有两个交点(如图),设它们的横坐标各是
的图象,可以看出这两个图象有两个交点(如图),设它们的横坐标各是![]() ,
,![]() ,其中
,其中![]() ,
,![]() .注意到
.注意到![]() 时,
时,![]() ,所以,等式
,所以,等式![]() 不成立.与①比较后知,方在①不存在区间
不成立.与①比较后知,方在①不存在区间![]() 内的根.由此可见,方程②只有一个大于1的正实根.
内的根.由此可见,方程②只有一个大于1的正实根.
由抛物线的轴对称性,可以看出,当内接等腰直角三角形处于图的状况时,斜边与抛物线的对称轴相交,有两解(见图).
类似地,当内接等腰直角三角形的斜边与抛物线的对称轴不相交时,又有两解.
综上可知,抛物线![]() 共有四个内接等腰直角三角形,它们过焦点的那条直角边的斜率恰是方程②的四个实根
共有四个内接等腰直角三角形,它们过焦点的那条直角边的斜率恰是方程②的四个实根

练习册系列答案
相关题目
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: ,
,![]() ,
,![]()

![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?