题目内容
【题目】如图,椭圆![]() 的右焦点为
的右焦点为![]() ,过焦点
,过焦点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点(异于长轴端点),
两点(异于长轴端点),![]() 是直线
是直线![]() 上的动点.
上的动点.

(1)若直线![]() 平分线段
平分线段![]() ,求证:
,求证:![]() .
.
(2)若直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,求实数
的斜率成等差数列,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用点差法可证得结论成立;
(2)令![]() ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,列出韦达定理,利用直线
的方程与椭圆的方程联立,列出韦达定理,利用直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,可得出
的斜率成等差数列,可得出![]() 关于
关于![]() 的等式,然后利用函数的基本性质可求得实数
的等式,然后利用函数的基本性质可求得实数![]() 的取值范围.
的取值范围.
(1)设![]() 、
、![]() ,线段
,线段![]() 的中点
的中点![]() ,由题意可得
,由题意可得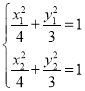 ,
,
上述两式相减得![]() ,可得
,可得![]() ,
,
![]() ,
,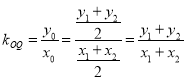 ,则
,则![]() ,
,
因此,![]() ;
;
(2)由![]() ,令
,令![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由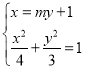 得
得![]() ,
,![]() 恒成立,
恒成立,
由韦达定理得![]() ,
,![]() ,
,
因为直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,
的斜率成等差数列,
所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,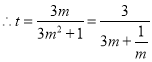 ,
,
由双勾函数的单调性可知,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,所以,
,所以,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目