题目内容
【题目】已知抛物线![]() :
:![]() ,点
,点![]() 是
是![]() 上的不同于顶点的动点,
上的不同于顶点的动点,![]() 上在点
上在点![]() 处的切线
处的切线![]() 分别与
分别与![]() 轴轴交于点
轴轴交于点![]() 、
、![]() .若存在常数
.若存在常数![]() 满足对任意的点
满足对任意的点![]() 都有
都有![]() .
.
(Ⅰ)求实数![]() ,
,![]() 的值;
的值;
(Ⅱ)过点![]() 作
作![]() 的垂线与
的垂线与![]() 交于不同于
交于不同于![]() 的一点
的一点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)先求导数,利用导数几何意义得切线斜率,根据点斜式得切线方程,即得![]() 、
、![]() 坐标,根据坐标化简
坐标,根据坐标化简![]() ,最后根据等式恒成立得
,最后根据等式恒成立得![]() ,
,![]() 的值;
的值;
(Ⅱ)先设![]() ,根据向量垂直坐标表示得
,根据向量垂直坐标表示得![]() 与
与![]() 横坐标关系,再根据两点间距离公式得
横坐标关系,再根据两点间距离公式得![]() 、
、![]() ,最后根据三角形面积公式得面积函数关系式,利用导数求其最值,即得结果.
,最后根据三角形面积公式得面积函数关系式,利用导数求其最值,即得结果.
(Ⅰ)设![]() ,则
,则![]() ,
,
![]()
![]() ,
,
即![]() .
.
![]() 分别与
分别与![]() 轴轴交于点
轴轴交于点![]() 、
、![]()
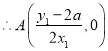 ,
,![]() .
.
![]()
![]() ,
,
∵存在常数![]() 满足对任意的点
满足对任意的点![]() 都有
都有![]() ∴
∴![]() .
.
(Ⅱ)设![]() ,
,![]()
![]()
![]()
![]()
∵![]() ,
,![]() ,故
,故![]() ,即
,即![]()
![]()
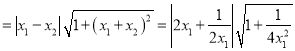
![]()
又![]() ,故
,故![]() 的面积为
的面积为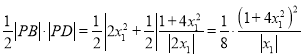
取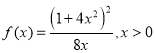 ,则
,则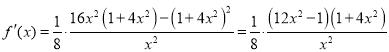 .
.
![]()
∴![]() 在
在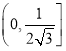 上是减函数,在
上是减函数,在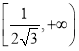 上是增函数.
上是增函数.
∴当![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.
故![]() 面积的最小值是
面积的最小值是![]() .
.

练习册系列答案
相关题目