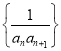题目内容
【题目】在△ABC中,角A,B,C所对的边分别是a,b,c,且![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() .
.
【答案】(Ⅰ)证明详见解析;(Ⅱ)4.
【解析】试题分析:(Ⅰ)将已知等式通分后利用两角和的正弦函数公式整理,利用正弦定理,即可证明.(Ⅱ)由余弦定理求出A的余弦函数值,利用(Ⅰ)的条件,求解B的正切函数值即可
试题解析:(1)根据正弦定理,设![]() =
=![]() =
=![]() =k(k>0).
=k(k>0).
则a="ksin" A,b="ksin" B,c="ksin" C.
代入![]() +
+![]() =
=![]() 中,有
中,有![]() +
+![]() =
=![]() ,变形可得
,变形可得
sin Asin B="sin" Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)="sin" C,
所以sin Asin B="sin" C.
(2)由已知,b2+c2–a2=![]() bc,根据余弦定理,有cos A=
bc,根据余弦定理,有cos A=![]() =
=![]() .
.
所以sin A=![]() =
=![]() .
.
由(Ⅰ),sin Asin B="sin" Acos B+cos Asin B,所以![]() sin B=
sin B=![]() cos B+
cos B+![]() sin B,
sin B,
故tan B=![]() =4.
=4.

练习册系列答案
相关题目
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()