题目内容
15.已知公差不为0的等差数列{an}的前3项和S3=9,且a1,a2,a5成等比数列.(1)求数列{an}的通项公式和前n项和Sn;
(2)设Tn为数列$\left\{{\frac{1}{{{S_{n+1}}-1}}}\right\}$的前n项和,求证:Tn<$\frac{3}{4}$.
分析 (1)由题意列式求得数列的首项和公差,然后代入等差数列的通项公式和前n项和公式得答案;
(2)求出数列$\left\{{\frac{1}{{{S_{n+1}}-1}}}\right\}$的通项,利用裂项相消法求出数列$\left\{{\frac{1}{{{S_{n+1}}-1}}}\right\}$的前n项和得答案.
解答 (1)解:设等差数列{an}的公差为d(d≠0),由S3=9,得3a1+3d=9,即a1+d=3.
又a1,a2,a5成等比数列,∴${a}_{1}({a}_{1}+4d)=({a}_{1}+d)^{2}$,整理得:d=2a1,
联立$\left\{\begin{array}{l}{{a}_{1}+d=3}\\{d=2{a}_{1}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$,
∴an=1+2(n-1)=2n-1,${S}_{n}=n+\frac{2n(n-1)}{2}={n}^{2}$;
(2)证明:$\frac{1}{{S}_{n+1}-1}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴${T}_{n}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})=\frac{3}{4}-\frac{2n+3}{2{n}^{2}+6n+4}$$<\frac{3}{4}$.
点评 本题考查了等比数列的通项公式,考查了等比数列的前n项和,训练了裂项相消法求数列的和,是中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | [$\frac{1}{3}$,$\frac{1}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$] |
| A. | $\frac{4}{3}$ | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |

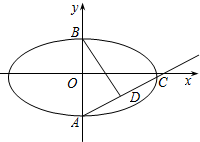 如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.
如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.