题目内容
12.已知∠AOB在平面α内,P∉α,且∠POA=∠POB,PH⊥α于H,求证:0H平分∠A0B.
分析 作HC⊥OA于C,HD⊥OB于D,连结PC、PD,证明△POC≌△POD.可得PC=PD,从而HC=HD.即可证明结论.
解答 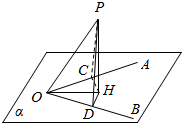 证明:作HC⊥OA于C,HD⊥OB于D,连结PC、PD,
证明:作HC⊥OA于C,HD⊥OB于D,连结PC、PD,
则PC⊥OA,PD⊥OB.
在Rt△POC和Rt△POD中,∠POA=∠POB.
∴△POC≌△POD.∴PC=PD.
∵HC、HD分别是PC、PD在平面α内的射影,
∴HC=HD.
于是0H平分∠A0B.
点评 本题考查线面垂直,考查三角形全等的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.若偶函数y=f(x),x∈R,满足f(x+2)=-f(x),且x∈[0,2]时,f(x)=3-x2,则方程f(x)=sin|x|在[-10,10]内的根的个数为( )
| A. | 12 | B. | 10 | C. | 9 | D. | 8 |
7.已知函数f(x)=x2-x+2,则${∫}_{0}^{1}$f(x)dx=( )
| A. | $\frac{13}{6}$ | B. | $\frac{11}{6}$ | C. | 2 | D. | 3 |