题目内容
17．求函数f（x）=x-0.2+2x0.5，的定义域为（0，+∞）．分析 化分数指数幂为根式，然后由题意可得$\left\{\begin{array}{l}{x＞0}\\{x≥0}\end{array}\right.$，求得x的范围得答案．
解答 解：f（x）=x-0.2+2x0.5=$\frac{1}{\root{10}{{x}^{2}}}+2\sqrt{x}$，
要使原函数有意义，则$\left\{\begin{array}{l}{x＞0}\\{x≥0}\end{array}\right.$，即x＞0．
∴函数f（x）=x-0.2+2x0.5的定义域为（0，+∞）．
故答案为：（0，+∞）．
点评 本题考查函数的定义域及其求法，考查了根式与分数指数幂的互化，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
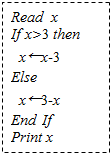如图是一个算法的伪代码，若输入x的值为1，则输出的x的值是2．