题目内容
2.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线为$y=\sqrt{3}x$,右焦点F(4,0),左右顶点分别为A1,A2,P为双曲线上一点(不同于A1,A2),直线A1P,A2P分别与直线x=1交于M,N两点;(1)求双曲线的方程;
(2)求证:$\overrightarrow{FM}•\overrightarrow{FN}$为定值,并求此定值.
分析 (1)利用焦距,离心率,列出方程组,求解即可.
(2)设出P,求出MN,然后求解数量积推出结果即可.
解答 解:(1)$\left\{\begin{array}{l}c=4\\ \frac{b}{a}=\sqrt{3}\\{c^2}={a^2}+{b^2}\end{array}\right.⇒\left\{\begin{array}{l}a=2\\ b=2\sqrt{3}\end{array}\right.⇒\frac{x^2}{4}-\frac{y^2}{12}=1$
(2)$设P({x_0},{y_0}),{A_1}P:y=\frac{y_0}{{{x_0}+2}}(x+2),{A_2}P:y=\frac{y_0}{{{x_0}-2}}(x-2)$,
所以$M(1,\frac{{3{y_0}}}{{{x_0}+2}}),N(1,\frac{{-{y_0}}}{{{x_0}-2}})$,
所以$\overrightarrow{FM}•\overrightarrow{FN}=(-3,\frac{{3{y_0}}}{{{x_0}+2}})•(-3,\frac{{-{y_0}}}{{{x_0}-2}})=9-\frac{{3{y_0}^2}}{{{x_0}^2-4}}=9-\frac{{3{y_0}^2}}{{\frac{{{y_0}^2}}{3}}}=0$.
点评 本题考查椭圆的标准方程的应用,考查直线与椭圆位置关系的应用,考查计算能力.

练习册系列答案
相关题目
17.若x,y∈[-$\frac{π}{2}$,$\frac{π}{2}$],且xsinx-ysiny>0,那么下面关系正确的是( )
| A. | x>y | B. | x+y>0 | C. | x<y | D. | x2>y2 |
11.已知函数$f(x)=\frac{4x}{{3{x^2}+3}}$,函数$g(x)=\frac{1}{3}a{x^3}-{a^2}x(a≠0)$,若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)=g(x2),则实数a的取值范围是( )
| A. | (0,+∞) | B. | $[\frac{1}{3},1]$ | C. | $[\frac{1}{3},+∞)$ | D. | (0,1] |
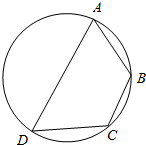 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论: