题目内容
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
【答案】(Ⅰ) ![]() (Ⅱ)见解析(III)见解析
(Ⅱ)见解析(III)见解析
【解析】试题分析:(Ⅰ)先利用焦点在![]() 轴上设出抛物线的方程,再代点进行求解;(Ⅱ)在抛物线上设点,利用斜率公式求相关直线的斜率,利用斜率和为0求出等量关系,进而可以证明;(III)利用斜率之积为定值得到等量关系,再写出直线的点斜式方程,进而得到结论.
轴上设出抛物线的方程,再代点进行求解;(Ⅱ)在抛物线上设点,利用斜率公式求相关直线的斜率,利用斜率和为0求出等量关系,进而可以证明;(III)利用斜率之积为定值得到等量关系,再写出直线的点斜式方程,进而得到结论.
试题解析:(Ⅰ)依题意,可设所求拋物线的方程为![]() ,
,
因拋物线过点![]() ,故
,故![]() ,拋物线的方程为
,拋物线的方程为![]() .
.
(Ⅱ)设![]() ,则
,则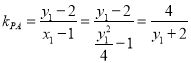 ,
,
同理![]()
![]() ,∴
,∴![]() ,
, ![]() .
.
![]() ,即直线
,即直线![]() 的斜率恒为定值,且值为
的斜率恒为定值,且值为![]() .
.
(III)![]() ,∴
,∴![]() ,∴
,∴![]() .
.
直线![]() 的方程为
的方程为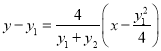 ,即
,即![]() .
.
将![]() 代入上式得
代入上式得![]() 即为直线
即为直线![]() 的方程,
的方程,
所以直线![]() 恒过定点
恒过定点![]() ,命题得证.
,命题得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目