Question

【题目】如图，已知三棱柱，侧面.

(Ⅰ)若分别是的中点，求证： ；

(Ⅱ)若三棱柱的各棱长均为2，侧棱与底面所成的角为，问在线段上是否存在一点，使得平面?若存在，求与的比值，若不存在，说明理由．

Answer 1

【答案】（1）见解析（2）2

【解析】试题分析：（1）由线面平行的判定定理证明，MN∥BC1，所以MN∥平面BCC1B1.（2）建立空间直角坐标系，利用空间向量求解。

试题解析：

解：(1)证明：连接AC1，BC1，

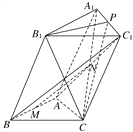
则AC1∩A1C＝N，AN＝NC1，

因为AM＝MB，所以MN∥BC1.

又BC1平面BCC1B1，

所以MN∥平面BCC1B1.

(2)作B1O⊥BC于O点，连接AO，

因为平面BCC1B1⊥底面ABC，

所以B1O⊥平面ABC，

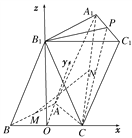
以O为原点，建立如图所示的空间直角坐标系，则A(0，，0)，B(－1，0,0)，C(1,0,0)，B1(0,0，)．由＝＝，可求出A1(1，，)，C1(2,0，)，

设点P(x，y，z)， ＝λ.

则P，

＝，

＝(－1,0，)．

设平面B1CP的法向量为n1＝(x1，y1，z1)，

由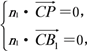

得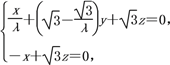

令z1＝1，解得n1＝.

同理可求出平面ACC1A1的法向量n2＝(，1，－1)．

由平面B1CP⊥平面ACC1A1，

得n1·n2＝0，即3＋－1＝0，

解得λ＝3，所以A1C1＝3A1P，

从而C1P∶PA1＝2.