题目内容
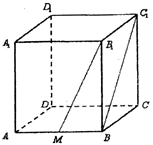
如图S为正三角形ABC所在平面外一点,且SA=SB=SC=AB,E、F分别为SC、AB中点,则异面直线EF与AB所成角为 ( )

| A.60º | B.90º | C.45º | D.30º |

C
先通过平移将两条异面直线平移到同一个起点SA的中点G,得到的锐角或直角就是异面直线所成的角,在三角形中再利用三角形的有关性质可得答案.
解:如图,取AS的中点G,连接GE、GF,∠GEF为异面直线EF与AC所成的角,
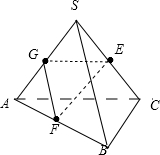
设棱长为2,则GE=1,GF=1,而EG⊥GF,
∴∠GEF=45°,
故选C

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目

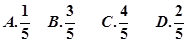
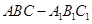 中,
中,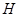 是正方形
是正方形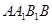 的中心,
的中心,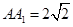 ,
,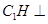 平面
平面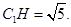
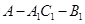 的正弦值;
的正弦值;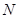 为棱
为棱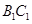 的中点,点
的中点,点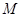 在平面
在平面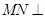 平面
平面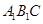 ,求线段
,求线段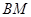 的长.
的长.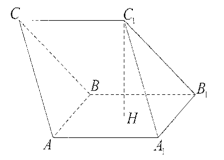
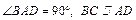 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.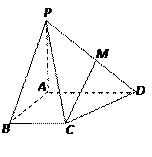
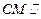 平面PAB;
平面PAB;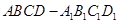 的侧棱长为2,
的侧棱长为2,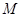 为
为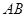 的中点,则异面直线
的中点,则异面直线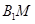 与
与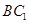 所成角的大小为( )
所成角的大小为( )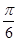
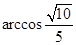
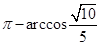
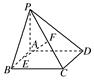
 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面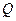 为AD的中点,
为AD的中点,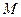 是棱
是棱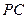 上的点,
上的点,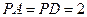 ,
,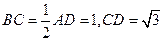 .(1)若
.(1)若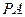
 ;(2)求证:平面
;(2)求证:平面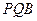 ⊥平面
⊥平面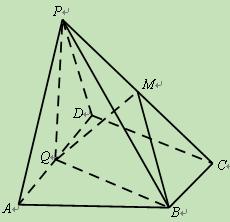
 C1的体积;
C1的体积;
 条直线把平面分成
条直线把平面分成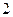 部分;
部分;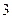 或
或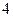 部分;
部分;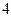 或
或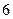 或
或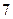 部分。类比空间
部分。类比空间