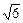题目内容
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,底面为直角梯形,
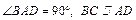 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.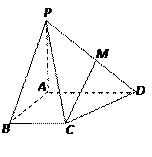
(Ⅰ)设M为PD的中点,求证:
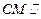 平面PAB;
平面PAB;(Ⅱ)求侧面PAB与侧面PCD所成二面角的平面角的正切值.
解法一:(Ⅰ)证明:取PA的中点N,连结BN、NM,在△PAD中,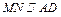 ,且
,且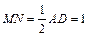 ;又
;又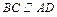 ,且
,且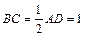 ,所以MN
,所以MN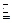 BC,即四边形BCMN为平行四边形,
BC,即四边形BCMN为平行四边形,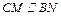 .又
.又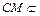 平面PAB,
平面PAB,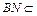 平面PAB,故
平面PAB,故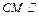 平面PAB. ……5分
平面PAB. ……5分
(Ⅱ)在平面ABCD中,AB与CD不平行,延长AB、CD交于一点,设为E,连结PE,则PE为侧面PAB与侧面PCD所成二面角的棱,又由题设可知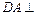 侧面PAB,于是过A作
侧面PAB,于是过A作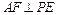 于F,连结DF,由三垂线定理可知
于F,连结DF,由三垂线定理可知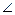 AFD为侧面PAB与侧面PCD所成二面角的平面角. ……8分
AFD为侧面PAB与侧面PCD所成二面角的平面角. ……8分
在△EAD中,由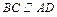 ,
, ,知B为AE为中点,∴AE=2,在Rt△PAE中,PA=1,AE=2,∴
,知B为AE为中点,∴AE=2,在Rt△PAE中,PA=1,AE=2,∴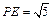 ,
,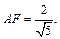 故
故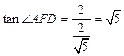 ,
,
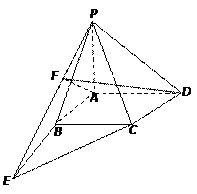 即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为
即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为 ……12分
……12分
解法二:以A为坐标原点,以AB、AD、AP所在直线为x、y、z轴建立如图所示的空间直角坐标系,则B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1). ……2分
(Ⅰ)由M为PD中点知M的坐标为(0,1,1),所以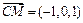 ,又平面PAB的法向量可取为
,又平面PAB的法向量可取为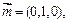 ∴
∴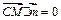 ,即
,即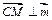 . 又
. 又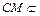 平面PAB,所以
平面PAB,所以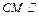 平面PAB. ……6分
平面PAB. ……6分
 (Ⅱ)设平面PCD的法向量为
(Ⅱ)设平面PCD的法向量为
∵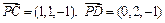 ,∴
,∴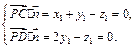
不妨取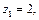 则
则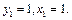 ∴
∴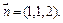
又平面PAB的法向量为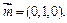
设侧面PAB与侧面PCD所成二面角的平面角大小为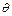 ,
,
则由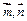 的方向可知
的方向可知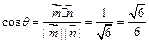 ,
,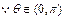 ,∴
,∴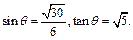
即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为 ……12分
……12分
(解法三:因为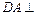 侧面PAB,
侧面PAB,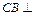 侧面PAB,所以也可以考虑用射影面积来求解)
侧面PAB,所以也可以考虑用射影面积来求解)
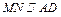 ,且
,且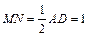 ;又
;又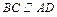 ,且
,且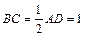 ,所以MN
,所以MN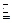 BC,即四边形BCMN为平行四边形,
BC,即四边形BCMN为平行四边形,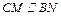 .又
.又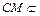 平面PAB,
平面PAB,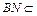 平面PAB,故
平面PAB,故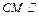 平面PAB. ……5分
平面PAB. ……5分(Ⅱ)在平面ABCD中,AB与CD不平行,延长AB、CD交于一点,设为E,连结PE,则PE为侧面PAB与侧面PCD所成二面角的棱,又由题设可知
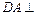 侧面PAB,于是过A作
侧面PAB,于是过A作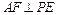 于F,连结DF,由三垂线定理可知
于F,连结DF,由三垂线定理可知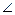 AFD为侧面PAB与侧面PCD所成二面角的平面角. ……8分
AFD为侧面PAB与侧面PCD所成二面角的平面角. ……8分在△EAD中,由
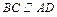 ,
, ,知B为AE为中点,∴AE=2,在Rt△PAE中,PA=1,AE=2,∴
,知B为AE为中点,∴AE=2,在Rt△PAE中,PA=1,AE=2,∴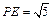 ,
,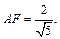 故
故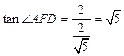 ,
, 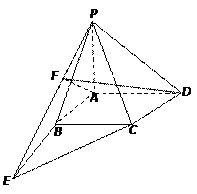 即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为
即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为 ……12分
……12分 |
解法二:以A为坐标原点,以AB、AD、AP所在直线为x、y、z轴建立如图所示的空间直角坐标系,则B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1). ……2分
(Ⅰ)由M为PD中点知M的坐标为(0,1,1),所以
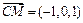 ,又平面PAB的法向量可取为
,又平面PAB的法向量可取为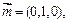 ∴
∴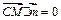 ,即
,即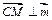 . 又
. 又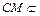 平面PAB,所以
平面PAB,所以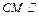 平面PAB. ……6分
平面PAB. ……6分 (Ⅱ)设平面PCD的法向量为
(Ⅱ)设平面PCD的法向量为
∵
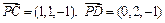 ,∴
,∴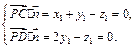
不妨取
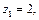 则
则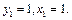 ∴
∴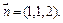
又平面PAB的法向量为
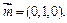
设侧面PAB与侧面PCD所成二面角的平面角大小为
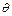 ,
,则由
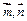 的方向可知
的方向可知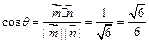 ,
,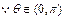 ,∴
,∴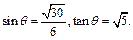
即所求侧面PAB与侧面PCD所成二面角的平面角的正切值为
 ……12分
……12分(解法三:因为
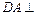 侧面PAB,
侧面PAB,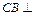 侧面PAB,所以也可以考虑用射影面积来求解)
侧面PAB,所以也可以考虑用射影面积来求解)略

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
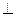 底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)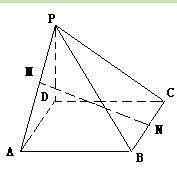
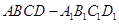 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高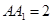 。求:
。求: 与
与 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示); 的体积。
的体积。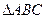 中,
中,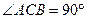 ,
,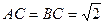 ,
,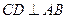 ,
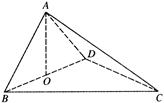
,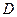 为垂足.沿
为垂足.沿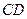 将
将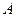 、
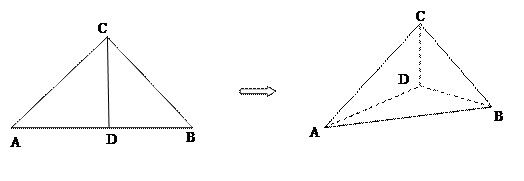
、 ,使得
,使得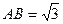 .
.
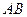 上是否存在点
上是否存在点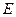 ,使
,使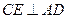 ?若存在,求出
?若存在,求出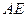 的长;若不存在,说明理由;
的长;若不存在,说明理由; 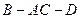 的平面角的大小.
的平面角的大小.
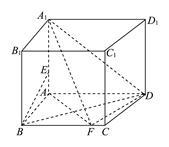
 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.