题目内容
【题目】已知关于![]() 的不等式
的不等式![]() .
.
(1)当![]() 时,解不等式;
时,解不等式;
(2)如果不等式的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)当![]() 时,不等式
时,不等式![]() 变为
变为![]() 。由绝对值的意义,按绝对值号内的
。由绝对值的意义,按绝对值号内的![]() 的正负,分三种情况讨论:当
的正负,分三种情况讨论:当![]() 时,不等式变为
时,不等式变为![]() ;当
;当![]() 时,不等式变为
时,不等式变为![]() ,恒成立,所以
,恒成立,所以![]() 符合不等式;当
符合不等式;当![]() 时,不等式变为
时,不等式变为![]() 。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数
。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数![]() 与
与![]() ,原不等式的解集为空集,
,原不等式的解集为空集, ![]() 的最小值比大于或等于
的最小值比大于或等于![]() ,作出
,作出![]() 与
与![]() 的图象. 只须
的图象. 只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合, ![]() 。解法二:构造函数
。解法二:构造函数![]() ,讨论绝对值号内式子得正负去掉绝对值可得,
,讨论绝对值号内式子得正负去掉绝对值可得, ![]()
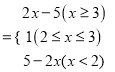 ,求每一段函数的值域,可得函数的最小值
,求每一段函数的值域,可得函数的最小值![]() =1,
=1, ![]() 小于等于函数的最小值1.解法三,由不等式
小于等于函数的最小值1.解法三,由不等式![]() 可得
可得![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.
试题解析:解:(1)原不等式变为![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]()
当![]() 时,原不等式化为
时,原不等式化为![]() ,∴
,∴ ![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]() .
.
综上,原不等式解集为![]() .
.
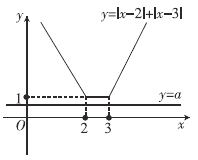
(2)解法一:作出![]() 与
与![]() 的图象.
的图象.
若使![]() 解集为空集,
解集为空集,
只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合,
∴![]() ,所以
,所以![]() 的范围为
的范围为![]() .
.
解法二: ![]()
 ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
综上![]() ,原问题等价于
,原问题等价于![]() ,∴
,∴ ![]() .
.
解法三:∵![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
