题目内容
16.已知一元二次方程x2+bx-2c=0,(b,c∈R)有两实根,其中一根x1∈(-1,0),另一根x2∈(0,1),则c+1b+2的取值范围是( )| A. | (14,13) | B. | (13,12) | C. | (13,1) | D. | (-∞,13)∪(1,+∞) |
分析 设f(x)=x2+bx-2c.利用根与系数之间的关系转化为不等式之间的关系,利用线性规划的知识进行求解即可.
解答 解:设f(x)=x2+bx-2c.
∵x2+bx-2c=0有两根x1,x2,x1∈(-1,0),x2∈(0,1)
∴{f(−1)>0f(0)<0f(1)>0,即{1−b−2c>0−2c<01+b−2c>0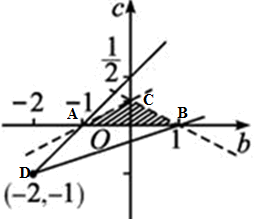
由点(b,c)满足的平面区域如图所示,
c+1b+2的几何意义为区域内的点与定点D(-2,-1)连线的斜率,
则由图象知AD的斜率最大,BD的斜率最小,
其中A(-1,0),B(1,0),
则AD的斜率k=0+1−1+2=1,BD的斜率k=0+11+2=13,
∴k∈(13,1).
故选:C
点评 本题主要考查线性规划的应用,根据根与系数之间的关系以及直线斜率公式是解决本题的关键.综合性较强.

练习册系列答案
相关题目
 的函数
的函数 ,若对任意的
,若对任意的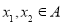 ,有
,有 ,则称函数
,则称函数 函数”,以下五个函数:①
函数”,以下五个函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,其中是“定义上的
,其中是“定义上的 函数”的有( )
函数”的有( )