题目内容
12.设数列{an}满足a1=2,am+n+am-n-m+n=$\frac{1}{2}$(a2m+a2n),其中m,n∈N,m≥n.(1)证明:对一切n∈N,都有an+2=2an+1-an+2.
(2)证明:$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$<1.
分析 (1)根据数列递推式,利用赋值法,可得a2,根据数列递推式,令m=n+2,进而可得an+2=2an+1-an+2;
(2)确定数列{an}的通项,运用裂项相消求出数列的和,再进行放缩,即可证得结论.
解答 (1)证明:令m=n,可得a0=0;令n=0,可得a2m=4am-2m,
令m=1,可得a2=4a1-2=6;
令m=n+2,则a2n+2+a2-2=$\frac{1}{2}$(a2n+4+a2n),
∵a2m=4am-2m,
∴a2n+1=4an+1-2(n+1),a2n+4=4an+2-2(n+2),a2n=4an-2n
∴an+2=2an+1-an+2;
(2)证明:由(1)知(an+2-an+1)-(an+1-an)=2
∵bn=an+1-an,
∴bn+1-bn=2
∴数列{bn}为首项为a2-a1=4,公差为2的等差数列,
bn=2n+2,
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=2+4+6+…+2n=n(n+1),
$\frac{1}{{a}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
即有$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$<1.
点评 点评:本题考查数列递推式,考查等差数列的证明,考查数列的通项与求和,考查不等式的证明,正确确定数列的通项,利用裂项相消求和及放缩法是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
1.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(9)+f(10)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
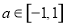 ,函数
,函数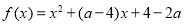 值总大于0,则
值总大于0,则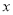 的取值范围是 .
的取值范围是 .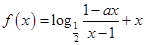 为奇函数,
为奇函数,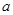 为常数.
为常数.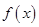 在
在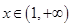 上的单调性,并说明理由;
上的单调性,并说明理由;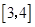 上的每一个
上的每一个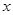 值,不等式
值,不等式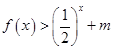 恒成立,求实数
恒成立,求实数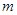 的取值范围.
的取值范围.