一艘船在海上由西向东航航行.在A处望见灯塔C在船的东北方向.半小时后在B处望见灯塔C在船的北偏东30°方向.航速为每小时30海里.当船到达D处时望见灯塔C在船的西北方向.求A.D两点间的距离．题目和参考答案——青夏教育精英家教网——

题目内容

19．一艘船在海上由西向东航航行，在A处望见灯塔C在船的东北方向，半小时后在B处望见灯塔C在船的北偏东30°方向，航速为每小时30海里，当船到达D处时望见灯塔C在船的西北方向，求A，D两点间的距离．

分析作CE⊥AD，根据AB=15，AE=DE，可求AE的长，从而求得AD的长．

解答解：由题意，如图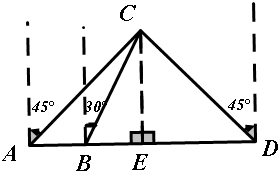，作CE⊥AD于点E．设AE=x，则CE=AE=DE=x，BE= $\frac{\sqrt{3}}{3}$ x，
∵AB=15，AE=DE，
∴x= $\frac{\sqrt{3}}{3}$ x+15，
∴x= $\frac{45+15\sqrt{3}}{2}$ ，AD=2x=45+15 $\sqrt{3}$
答：A、D两地的距离为45+15 $\sqrt{3}$ 海里．

点评本题考查求两点间的距离，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线，解直角三角形．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

9．设△ABC是锐角三角形，a，b，c分别是内角A，B，C所对边长，并且sin²A=sin（

\frac{π}{3}

$\frac{π}{3}$ +B）sin（

\frac{π}{3}

$\frac{π}{3}$ -B）+sin²B；
（1）求角A的大小；
（2）若b=2，c=1，D为BC的中点，求AD的长．

$\frac{co{s}^{2}α-si{n}^{2}α}{2tan（\frac{π}{4}-α）co{s}^{2}（\frac{π}{4}-α）}$ =1．

7．在数列{a_n}中，a₁=1，

$\frac{{a}_{n+1}+{a}_{n}}{{a}_{n+1}-{a}_{n}}$ =2n，求数列{a_n}的通项公式．

14．已知f（x）是定义在R上的偶函数，且f（x+2）=f（x），x∈R，当x∈（0，1）时，f（x）=2^x-1，则f（log₂12）的值为

$\frac{1}{3}$ ．

4．飞机的航线和山顶在同一个铅直平面内，已知飞机的高度为海波25000米，速度为3000米/分，飞行员先在点A看到山顶C的俯角为30°，经过8分钟后到达点B，此时看到山顶C的俯角为60°，则山顶的海拔高度为多少米．（参考数据：

$\sqrt{2}$ =1.414，

$\sqrt{3}$ =1.732，

$\sqrt{6}$ =2.449）．

11．已知数列{a_n}满足a_n+1=2a_n+3×2ⁿ，a₁=2，求数列{a_n}的通项公式．

8．已知数列{a_n}中，a₁=1且n＞1时，2S_n²=2a_nS_n-a_n，求a_n．

9．七位同学站成一排，甲、乙、丙三位同学不能相邻的排法共有多少种？