题目内容
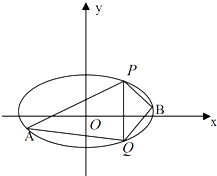
【题目】已知双曲线实轴长为6,一条渐近线方程为4x﹣3y=0.过双曲线的右焦点F作倾斜角为 ![]() 的直线交双曲线于A、B两点
的直线交双曲线于A、B两点
(1)求双曲线的方程;
(2)求线段AB的中点C到焦点F的距离.
【答案】
(1)解:由题得2a=6, ![]() ,
,
得a=3,b=4,
可得双曲线方程为 ![]()
(2)解:由题意可得F(5,0),直线AB的方程为y=x﹣5,
联立 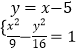 ,
,
消去y,可得7x2+90x﹣369=0,
设A(x1,y1),B(x2,y2),可得 ![]() ,
,
可得中点C的横坐标为 ![]() ,
,
可得C(﹣ ![]() ,﹣
,﹣ ![]() ),
),
F点横坐标为x=5,可得F(5,0),
即有|CF|= ![]() =
= ![]()
【解析】(1)运用双曲线的渐近线方程可得 ![]() ,结合条件2a=6,可得a,b,进而得到双曲线的方程;(2)求得直线AB的方程,代入双曲线的方程,消去y,可得x的方程,运用韦达定理和中点坐标公式可得C的坐标,再由两点的距离公式计算即可得到所求值.
,结合条件2a=6,可得a,b,进而得到双曲线的方程;(2)求得直线AB的方程,代入双曲线的方程,消去y,可得x的方程,运用韦达定理和中点坐标公式可得C的坐标,再由两点的距离公式计算即可得到所求值.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】为了解某班学生喜爱体育运动是否与性别相关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱体育运动 | 不喜爱体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部女生中随机调查2人,恰好调查到的2位女生都喜爱体育运动的概率为 ![]()
(1)请将上面的列联表补充完整(不用写计算过程)
(2)能偶在犯错误的概率不超过0.005的前提下认为喜爱体育运动与性别有关?说明你的理由;
下面的临界值表供参考:
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .其中n=a+b+c+d)
.其中n=a+b+c+d)