题目内容
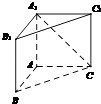
【题目】在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AC=BC=AA1=2，D、E分别为棱AB、BC的中点，点F在棱AA1上． 
（1）证明：直线A1C1∥平面FDE；
（2）若F为棱AA1的中点，求三棱锥A1﹣DEF的体积．
【答案】
（1）证明：直三棱柱ABC﹣A1B1C1中，D、E分别为棱AB、BC的中点，
∴DE∥AC，
又A1C1∥AC，
∴A1C1∥DE；
又DE平面FDE，A1C1平面FDE，
∴直线A1C1∥平面FDE
（2）解：如图所示：
当F为棱AA1的中点时，AF= 
AA1=1，
三棱锥A1﹣ADE的体积为
= 
S△ADEAA1= × DEECAA1= 
×1×1×2= ，
三棱锥F﹣ADE的体积为
VF﹣ADE= S△ADEAF= × DEEC AA1= ；
∴三棱锥A1﹣DEF的体积为
﹣VF﹣ADE= ﹣ = ．
【解析】（1）根据题意，证明DE∥AC，再证A1C1∥DE，从而证明直线A1C1∥平面FDE；（2）利用三棱锥A1﹣DEF的体积为 
﹣VF﹣ADE，即可求出结果．
【考点精析】掌握直线与平面平行的判定是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
字词句篇与同步作文达标系列答案
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | | | |||
f（x） | 0 | 3 | 0 | ﹣3 | 0 |
（1）请将表中数据补充完整，并直接写出函数f（x）的解析式；
（2）若将函数f（x）的图象上所有点的横坐标变为原来的2倍，纵坐标不变，得到函数g（x）的图象，求当x∈[﹣ 
， ]时，函数g（x）的值域；
（3）若将y=f（x）图象上所有点向左平移θ（θ＞0）个单位长度，得到y=h（x）的图象，若=h（x）图象的一个对称中心为（ 
），求θ的最小值．
