Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，离心率等于 ，它的一个短轴端点是（0，2 ）．

（1）求椭圆C的方程；
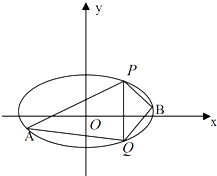
（2）P（2，3）、Q（2，﹣3）是椭圆上两点，A、B是椭圆位于直线PQ两侧的两动点，
①若直线AB的斜率为 ，求四边形APBQ面积的最大值；
②当A、B运动时，满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由．

Answer 1

【答案】
（1）解：∵椭圆C的中心在原点，焦点在x轴上，∴设椭圆C方程为 （a＞b＞0），

∵离心率等于 ，它的一个短轴端点是（0，2 ），

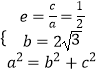∴ ，解得a=4，b=2 ，c=2，

∴椭圆C的方程为

（2）解：①设A（x1，y1），B（x2，y2），直线AB的方程为y= ，

代入 ，得：x2+tx+t2﹣12=0，

由△＞0，解得﹣4＜t＜4．由韦达定理得x1+x2=﹣t， ．

四边形APBQ的面积S= =9 ，

∴当t=0时， ．

②当∠APQ=∠BPQ，则PA、PB的斜率之和为0，设直线PA的斜率为k，则PB的斜率为﹣k，

PA的直线方程为y﹣3=k（x﹣2），

由 ，整理得：（9+4k2）x2+8（9﹣2k）kx+4（9﹣2k）2﹣48=0，

有 ．

同理PB的直线方程为y﹣9=﹣k（x﹣2），得 ，

∴ ， ．

从而kAB= = = = ，

∴AB的斜率为定值

【解析】（1）设椭圆C方程为 （a＞b＞0），由离心率等于 ，它的一个短轴端点是（0，2 ），列出方程组求出a，b，由此能求出椭圆C的方程．（2）①设直线AB的方程为y= ，代入 ，得：x2+tx+t2﹣12=0，由此利用根的判别式、韦达定理，弦长公式，能求出四边形APBQ面积的最大值．②当∠APQ=∠BPQ，则PA、PB的斜率之和为0，设直线PA的斜率为k，则PB的斜率为﹣k，PA的直线方程为y﹣3=k（x﹣2），PB的直线方程为y﹣9=﹣k（x﹣2），由此利用韦达定理结合已知条件能求出AB的斜率为定值 ．