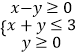��Ŀ����
����Ŀ��Ϊ�˽�ij��ѧ��ϲ�������˶��Ƿ����Ա���أ��Ա���50�˽������ʾ�����õ������µ���������
ϲ�������˶� | ��ϲ�������˶� | �ϼ� | |
���� | 5 | ||
�� | 10 | ||
�ϼ� | 50 |
��֪��ȫ��Ů�����������2�ˣ�ǡ�õ��鵽��2λŮ����ϲ�������˶��ĸ���Ϊ ![]()
��1���뽫�������������������������д������̣�
��2����ż�ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊϲ�������˶����Ա��йأ�˵��������ɣ�
������ٽ�ֵ�����ο���
P��K2��k�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��K2= ![]() ������n=a+b+c+d��
������n=a+b+c+d��
���𰸡�
��1���⣺��Ů������n�ˣ��� ![]() =
= ![]() ����n=25
����n=25
���������£�
ϲ�������˶� | ��ϲ�������˶� | �ϼ� | |
���� | 20 | 5 | 25 |
�� | 10 | 15 | 25 |
�ϼ� | 30 | 20 | 50 |
��2���⣺K2= ![]() =8.333��7.879��
=8.333��7.879��
���ڷ�����ĸ��ʲ�����0.005��ǰ������Ϊϲ�������˶����Ա��йأ�
����������1��������ȫ��Ů�����������2�ˣ�ǡ�õ��鵽��2λŮ����ϲ�������˶��ĸ���Ϊ ![]() �����ȫ��Ů�����������ɵõ�����������2�����ݹ�ʽ����K2 �� �����ٽ�ֵ�������ۣ�
�����ȫ��Ů�����������ɵõ�����������2�����ݹ�ʽ����K2 �� �����ٽ�ֵ�������ۣ�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�����Ŀ���������������������������������࣬������ȾΣ�����أ�������Ⱦ�������ļ¡��������ѵ��ķμ�����Ϊ�˽�ij���ķμ����Ƿ����Ա��йأ���ijҽԺ����Ķ���Ժ50�˽������ʾ����飬�õ����µ���������
���ķμ��� | �����ķμ��� | �ϼ� | |
�� | 5 | ||
Ů | 10 | ||
�ϼ� | 50 |
��֪��ȫ��50���������ȡ1�ˣ��鵽���ķμ������˵ĸ���Ϊ ![]() ��
��
��1���뽫���������������������
��2���Ƿ���99.5%�İ�����Ϊ���ķμ������Ա��йأ�˵��������ɣ�
��3����֪�ڻ��ķμ�����10λŮ���У���3λ�ֻ���θ�������ڴӻ��ķμ�����10λŮ���У�ѡ��3����������������Ų飬��ѡ����θ����Ů������Ϊ�Σ���εķֲ��С���ѧ�����Լ����
������ٽ�ֵ�������ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |