题目内容
【题目】函数f（x）=Asin（ωx+）（ 
）的部分图象如图所示． 
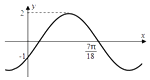
（1）求函数f（x）的解析式．
（2）函数y=f（x）的图象可以由y=sinx的图象变换后得到，请写出一种变换过程的步骤（注明每个步骤后得到新的函数解析式）．
【答案】
（1）解：由函数图象可得：A=2，f（0）=﹣1，
∴ 
，
∵ 
，
∴ 
，
∵ 
，
∴ 
，
∴ 
，
∵ 
，
∴k=1，ω=3，
∴ 
．
（2）解：把y=sinx（x∈R）的图象向右平移 
个单位，可得y=sin（x﹣ ）的图象；
把所得图象上各点的横坐标变为原来的 
倍，可得y=sin（3x+ ）的图象；
再把所得图象上各点的纵坐标变为原来的2倍，可得y=2sin（3x+ ）的图象．
（三步每步表述及解析式正确各2分，前面的步骤错误，后面的正确步骤分值减半）．
【解析】（1）由函数图象得A=2， 
，结合范围 
，可求，由 
，结合 
，可求ω，即可得解函数解析式．（2）由题意利用y=Asin（ωx+φ）的图象变换规律，得出结论．
【考点精析】解答此题的关键在于理解函数y=Asin（ωx+φ）的图象变换的相关知识，掌握图象上所有点向左（右）平移
个单位长度，得到函数
的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的
倍（纵坐标不变），得到函数
的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的
倍（横坐标不变），得到函数
的图象．
期末集结号系列答案【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x | | | |||
f（x） | 0 | 3 | 0 | ﹣3 | 0 |
（1）请将表中数据补充完整，并直接写出函数f（x）的解析式；
（2）若将函数f（x）的图象上所有点的横坐标变为原来的2倍，纵坐标不变，得到函数g（x）的图象，求当x∈[﹣ 
， ]时，函数g（x）的值域；
（3）若将y=f（x）图象上所有点向左平移θ（θ＞0）个单位长度，得到y=h（x）的图象，若=h（x）图象的一个对称中心为（ 
），求θ的最小值．
【题目】近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病，为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查，得到如下的列联表．
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为 
，
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；
（3）已知在患心肺疾病的10位女性中，有3位又患有胃病，现在从患心肺疾病的10位女性中，选出3名进行其它方面的排查，记选出患胃病的女性人数为ξ，求ξ的分布列、数学期望以及方差．
下面的临界值表仅供参考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
