题目内容
18. 如图,在0~1随机选择两个数x,y,这两个数对应的点把0~1的线段分成了三条线段a,b,c,则这三条线段a,b,c能构成三角形的概率为( )
如图,在0~1随机选择两个数x,y,这两个数对应的点把0~1的线段分成了三条线段a,b,c,则这三条线段a,b,c能构成三角形的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 由已知,其中两段的长度分别为a,b,分别表示出线段随机地折成3段的a,b的约束条件和3段构成三角形的约束条件,再画出约束条件表示的平面区域,利用面积测度即可求出构成三角形的概率
解答  解:设三段长分别为a,b,c,则c=1-a-b,
解:设三段长分别为a,b,c,则c=1-a-b,
则总样本空间为 $\left\{\begin{array}{l}{0<a<1}\\{0<b<1}\\{a+b<1}\end{array}\right.$,所表示的平面区域为三角形OAB,其面积为 $\frac{1}{2}$,
能构成三角形的事件的空间为 $\left\{\begin{array}{l}{a+b>1-a-b}\\{a+1-a-b>b}\\{b+1-a-b>a}\end{array}\right.$,所表示的平面区域为三角形DEF,其面积为 $\frac{1}{8}$,
则所求概率为$\frac{{S}_{△DEF}}{{S}_{△AOB}}=\frac{\frac{1}{8}}{\frac{1}{2}}=\frac{1}{4}$.
故选:C.
点评 本题考查几何概型,对于几何概型的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.函数g(x)=x3+($\frac{m}{2}$+2)x2-2x在(2,3)上总存在极值,则实数m的取值范围为( )
| A. | (-$\frac{58}{9}$,-6) | B. | (-$\frac{37}{3}$,-9) | C. | (-$\frac{37}{3}$,9) | D. | (-$\frac{37}{3}$,-6) |
6.如图给出的是计算1+3+5+…+99的一个程序框图,其中判断内应填入的条件是( )


| A. | i<99 | B. | i>99 | C. | i<100 | D. | i>100 |
 将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.
将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.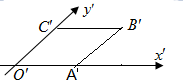 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )