题目内容
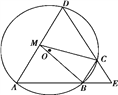
【题目】如图,四边形ABCD是☉O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(Ⅰ)证明:∠D=∠E;
(Ⅱ)设AD不是☉O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由四点共圆性质可得∠D=∠CBE.再结合条件∠CBE=∠E,得证(2)由等腰三角形性质得OM⊥AD,即得AD∥BC, 因此∠A=∠CBE=∠E.而∠D=∠E,所以△ADE为等边三角形.
试题解析:解: 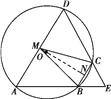 (1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.
(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.
由已知得∠CBE=∠E,故∠D=∠E.
(2)设BC的中点为N,连结MN,则由MB=MC知MN⊥BC,故O在直线MN上.又AD不是☉O的直径,M为AD的中点,故OM⊥AD,
即MN⊥AD. 所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E.由(1)知,∠D=∠E,所以△ADE为等边三角形.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】(本小题满分12分)某中学欲制定一项新的制度,学生会为此进行了问卷调查,所有参与问卷调查的人中,持有“支持”、“不支持”和“既不支持也不反对”的人数如下表所示:
支持 | 既不支持也不反对 | 不支持 | |
高一学生 | 800 | 450 | 200 |
高二学生 | 100 | 150 | 300 |
(Ⅰ)在所有参与问卷调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持”的人中抽取了45人,求
个人,已知从“支持”的人中抽取了45人,求![]() 的值;
的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人,从这5人中任意选取2人,求至少有1人是高一学生的概率.
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,下表是初赛成绩(得分均为整数,满分为100分)的频率分布表.
分组(分数段) | 频数(人数) | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
(Ⅰ)求频率分布表中![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答3道判断题,答对3道题获得一等奖,答对2道题获得二等奖,答对1道题获得三等奖,否则不得奖.若某同学进入决赛,且其每次答题回答正确与否均是等可能的,试列出他回答问题的所有可能情况,并求出他至少获得二等奖的概率.