��Ŀ����
����Ŀ������С������12�֣�ij��ѧ���ƶ�һ���µ��ƶȣ�ѧ����Ϊ�˽������ʾ����飬���в����ʾ���������У�������֧����������֧���������Ȳ�֧��Ҳ�����������������±���ʾ��
֧�� | �Ȳ�֧��Ҳ������ | ��֧�� | |
��һѧ�� | 800 | 450 | 200 |
�߶�ѧ�� | 100 | 150 | 300 |
�����������в����ʾ���������У��÷ֲ�����ķ�����ȡ![]() ���ˣ���֪����֧���������г�ȡ��45�ˣ���
���ˣ���֪����֧���������г�ȡ��45�ˣ���![]() ��ֵ��
��ֵ��
�������ڳ�����֧����̬�ȵ����У��÷ֲ�����ķ�����ȡ5�ˣ�����5��������ѡȡ2�ˣ���������1���Ǹ�һѧ���ĸ���.
���𰸡�������100�������� ![]() .
.
���������������������������֧�ֵ�����������ȡ��������������ȣ��������������������
������������֧����̬�ȵĹ���500�ˣ�������Ϊ�ٷ�֮һ��ȷ�����и�һ���߶���������Ȼ����ݹŵ���ͺŵĸ��ʹ�ʽ���.
����������⣺��1�����ݷֲ������ԭ����ÿ���ȡ�������ı�������ȵģ�������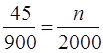 �����
�����![]() ��
��
��2�������⣺��һ���߶�������֧����̬�ȵĹ���500�ˣ�������Ϊ�ٷ�֮һ�����Գ�ȡ��5���У��и�һѧ��2�ˣ���Ϊ![]() �߶�ѧ��3�ˣ���Ϊ
�߶�ѧ��3�ˣ���Ϊ![]() ������5������ѡ2�ˣ���10�ֲ�ͬ�Ľ���������ǣ�
������5������ѡ2�ˣ���10�ֲ�ͬ�Ľ���������ǣ� ![]() .����������ѡȡ�ģ�����ÿ��������ֵĿ���������ȵģ����¼�AΪ��������һ���Ǹ�һѧ���������¼�A����
.����������ѡȡ�ģ�����ÿ��������ֵĿ���������ȵģ����¼�AΪ��������һ���Ǹ�һѧ���������¼�A����![]() ��7��������������ݹŵ���͵ĸ��ʹ�ʽ���¼�A�����ĸ���
��7��������������ݹŵ���͵ĸ��ʹ�ʽ���¼�A�����ĸ���![]()