题目内容
【题目】设{an}是正项等比数列，令Sn=lga1+lga2+…+lgan ， n∈N* ， 若存在互异的正整数m，n，使得Sm=Sn ， 则Sm+n= ．
【答案】0
【解析】解：∵{an}是正项等比数列，设公比为q，
∴lgan+1﹣lgan=lgq
∴数列{lgan}为等差数列，
设公差为d
则Sm=mlga1+ 
，Sn=nlga1+ 
∵Sm=Sn ，
∴Sm﹣Sn=mlga1+ ﹣nlga1﹣ =（m﹣n）（lga1+ 
）=0
∵m≠n
∴lga1+ ）=0
∴Sm+n=（m+n）lga1+ 
=（m+n）（lga1+ ）=0
所以答案是0．
【考点精析】掌握等比数列的前n项和公式和等比数列的基本性质是解答本题的根本，需要知道前
项和公式：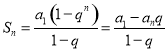
；{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列．
练习册系列答案
相关题目
【题目】某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如下图：
（1）记事件
为：“从这批小龙虾中任取一只，重量不超过35
的小龙虾”，求
的估计值；
（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；
（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
等级 | 一等品 | 二等品 | 三等品 |
重量（ |
|
|
|
按分层抽样抽取10只，再随机抽取3只品尝，记
为抽到二等品的数量，求抽到二级品的期望．