题目内容
7.设关于x的两个方程x2-ax+1=0,x2-bx+1=0的四个根组成以2为公比的等比数列,则ab=$\frac{27}{4}$.分析 根据等比数列的性质结合一元二次方程根与系数之间的关系进行求解.
解答 解:设以2为公比成等比数列的四个根依次为m,2m,4m,8m(m≠0).
则根据等比数列的性质可得m•8m=2m•4m,
∵两方程的常数项均为1,
∴m•8m=2m•4m=1,
即m2=$\frac{1}{8}$.
不妨设m、8m是方程x2-ax+1=0的两根,
而2m、4m是方程x2-bx+1=0的两根,
则a=m+8m=9m,b=2m+4m=6m
则ab=9m×6m=54m2=$\frac{1}{8}$×54=$\frac{27}{4}$.
故答案为:$\frac{27}{4}$
点评 本题主要考查等比数列的性质的应用,结合一元二次方程根与系数之间的关系是解决本题的关键.

练习册系列答案
相关题目
17.5人排成一排,甲只能排在第一个或第二两个位置,乙只能排在第二或第三两个位置,不同的排法共有( )
| A. | 12种 | B. | 16种 | C. | 18种 | D. | 24种 |
15.在△ABC中,内角A,B,C所对的边分别是a,b,c,B=60°,a+c=1,则b的取值范围为( )
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{1}{4}$,1) | C. | [$\frac{1}{4}$,$\frac{1}{2}$) | D. | (0,1) |
2.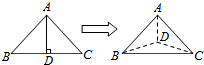 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
19.若θ是△ABC的一个内角,且sinθcosθ=$\frac{1}{8}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
16. 棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
 棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )| A. | 3$\sqrt{6}$ | B. | 8 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
 如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.
如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.