题目内容
11.已知不等式(a-1)x2-2$\sqrt{2}$xy+ay2≥0对一切正数x、y恒成立,则实数a的最小值是2.分析 先将原不等式变形,通过换元法结合二次函数的性质,得到不等式组,解出即可.
解答 解:∵x>0,y>0,
∴(a-1)x2-2$\sqrt{2}$xy+ay2≥0
?2$\sqrt{2}$xy≤(a-1)x2+ay2
?(a-1)${(\frac{x}{y})}^{2}$-2$\sqrt{2}$×$\frac{x}{y}$+a≥0,
令t=$\frac{x}{y}$(t>0),f(t)=(a-1)t2-2$\sqrt{2}$t+a,
依题意:$\left\{\begin{array}{l}{a-1>0}\\{f(\frac{\sqrt{2}}{a-1})≥0}\end{array}\right.$,
即:$\left\{\begin{array}{l}{a>1}\\{(a-1{)(\frac{\sqrt{2}}{a-1})}^{2}-2\sqrt{2}×\frac{\sqrt{2}}{a-1}+a≥0}\end{array}\right.$,
解得a≥2
∴实数a的最小值为2,
故答案为:2.
点评 本题考查函数恒成立问题,考查转化与构造函数思想,考查解不等式组的能力,属中档题.

练习册系列答案
相关题目
2.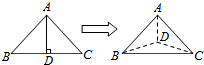 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
19.执行如图的程序框图,如果输入的N=10,那么输出的S=( )


| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | ||
| C. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{10×9×…×3×2×1}$ | D. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{11×10×…×3×2×1}$ |
6.利用计算机产生0~1之间的均匀随机数a,b,则事件“$\left\{\begin{array}{l}{3a-1>0}\\{3b-1>0}\end{array}\right.$”发生的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
3.如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )


| A. | 在区间(-2,1)内f(x)是增函数 | B. | 在(1,3)内f(x)是减函数 | ||
| C. | 在(4,5)内f(x)是增函数 | D. | 在x=2时f(x)取到极小值 |
 如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.
如图,某单位准备绿化一块直径AB=a的半圆形空地,△ABC以外地方种草,△ABC的内接正方形PQMN为一水池,其余的地方种花,设∠BAC=θ,△ABC的面积为S1,正方形PQMN的面积为S2.