题目内容
5．正方体ABCD-A1B1C1D1中，异面直线AC和A1D所成角的余弦为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 0 |
分析 画出图形，连接A1C1，C1D，则可说明∠DA1C1为异面直线AC与A1D所成角，并能判断△A1DC1为等边三角形，从而便能得出异面直线AC和A1D所成角的余弦值．
解答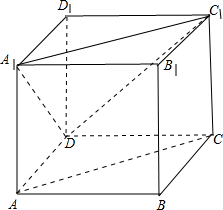 
解：如图，
连接A1C1，C1D，则AC∥A1C1；
∴∠DA1C1或其补角为异面直线AC和A1D所成角；
显然△A1DC1为等边三角形；
∴∠DA1C1=60°；
∴异面直线AC和A1D所成角的余弦值为$\frac{1}{2}$．
故选：A．
点评 考查异面直线所成角的概念及求法，正方体各面上的对角线相等．
练习册系列答案
相关题目
13．已知圆C的方程为x2+y2+2x-8=0，则圆C关于点（1，-2）对称的圆的方程为（ ）
| A． | （x+2）2+（y+2）2=9 | B． | （x+2）2+（y+2）2=3 | C． | （x-3）2+（y+4）2=9 | D． | （x-3）2+（y+4）2=3 |
20．已知△ABC中，$\overrightarrow{AB}+\overrightarrow{AC}=λ（\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|}}）$，则三角形的形状一定是（ ）
| A． | 等腰三角形 | B． | 等边三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
如图，四棱锥P-ABCD中，底面是直角梯形，AD∥BC，AB⊥AD，PA⊥底面ABCD，PA=AD=4，AB=1，BC=2，过A作AM⊥PC交PC于M．
14．在如下的2×2列联表中，若分类变量X和Y有关系，比值相差大的应该是（ ）
| X1 | X2 | 总计 | |
| Y1 | a | b | a+b |
| Y2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| A． | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B． | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C． | $\frac{a}{a+d}$与$\frac{c}{b+c}$ | D． | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |