题目内容
10. 如图,四棱锥P-ABCD中,底面是直角梯形,AD∥BC,AB⊥AD,PA⊥底面ABCD,PA=AD=4,AB=1,BC=2,过A作AM⊥PC交PC于M.
如图,四棱锥P-ABCD中,底面是直角梯形,AD∥BC,AB⊥AD,PA⊥底面ABCD,PA=AD=4,AB=1,BC=2,过A作AM⊥PC交PC于M.(1)判断AM与平面PCD是否垂直,并说明理由;
(2)AM与平面PBC所成的角是否大于30°?请说明理由.
分析 (1)可以采用反证法:假设AM与平面PCD垂直,那么AM⊥CD,那么CD垂直于平面PAC,CD⊥AC,事实通过勾股定理得出AC和CD是不垂直的,
(2)首先证明AN垂直于平面PBC,然后求出AM和AN的长度,求出线面夹角可得答案.
解答 解:(1)AM与平面PCD不垂直,理由如下:
假设AM⊥平面PCD,
∵CD?平面PCD,
∴AM⊥CD,
又∵PA⊥底面ABCD,CD?⊥底面ABCD,
∴PA⊥CD,
又由PA∩AM=A,PA,AM?平面PAC,
∴CD⊥平面PAC,
又∵AC?平面PAC,
∴CD⊥AC,
在直角梯形ABCD中,AD=4,AB=1,BC=2,AB⊥AD,
故AC=CD=$\sqrt{5}$,由勾股定理得出AC和CD是不垂直的,
故假设不成立,
即AM与平面PCD不垂直;
(2)AM与平面PBC所成的角小于30°,理由如下:
过A作AN⊥PB,垂足为N,
又∵PA⊥底面ABCD,BC?⊥底面ABCD,
∴PA⊥BC,
在直角梯形ABCD中,AB⊥BC,
又由PA∩AB=A,PA,AB?平面PAB,
∴BC⊥平面PAB,
又∵AN?平面PAB,
∴BC⊥AN,
∵PB∩BC=B,PB,BC?平面PBC,
∴AN⊥平面PBC,
∵PA=AD=4,AB=1,BC=2,
∴AN=$\frac{4}{\sqrt{17}}$,AM=$\frac{4\sqrt{5}}{\sqrt{21}}$,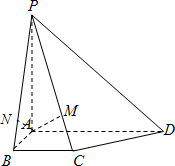
设AM与平面PBC所成的角为α,则cosα=$\frac{AN}{AM}$=$\sqrt{\frac{21}{85}}$<$\frac{\sqrt{3}}{2}$,
故AM与平面PBC所成的角小于30°.
点评 本题考查的知识点是空间线面垂直与线线垂直的判断与证明,求二面角,是立体几何知识的简单综合应用,难度中档.

 口算能手系列答案
口算能手系列答案| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x-y=0对称 | D. | 关于直线x+y=0对称 |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A. | 105 | B. | 51.5 | C. | 52 | D. | 52.5 |
得到下面的散点图及一些统计量的值.
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})({y}_{i}-\overline{y)}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.

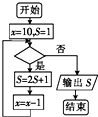
| A. | x>7? | B. | x>6? | C. | x≥6? | D. | x≤6? |
 如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分(y≥0),A是曲线C1和C2的交点.已知∠AF2F1为钝角且|AF1|=$\frac{7}{2}$,|AF2|=$\frac{5}{2}$.