题目内容
数列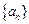 满足
满足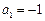 ,
,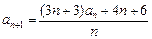 .(1)求
.(1)求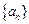 通项公式
通项公式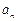 ;(2)令
;(2)令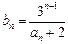 ,数列
,数列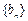 前
前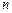 项和为
项和为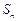 ,求证:当
,求证:当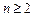 时,
时,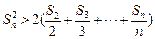 ;(3)证明:
;(3)证明: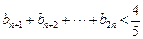 .
.
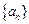 满足
满足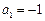 ,
,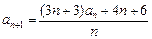 .(1)求
.(1)求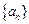 通项公式
通项公式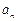 ;(2)令
;(2)令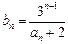 ,数列
,数列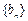 前
前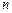 项和为
项和为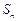 ,求证:当
,求证:当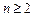 时,
时,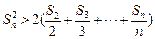 ;(3)证明:
;(3)证明: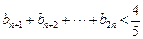 .
.(Ⅰ) 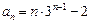 (Ⅱ)见解析 (Ⅲ)见解析
(Ⅱ)见解析 (Ⅲ)见解析
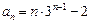 (Ⅱ)见解析 (Ⅲ)见解析
(Ⅱ)见解析 (Ⅲ)见解析(1)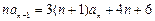 ,两边同除以
,两边同除以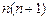 得:
得:
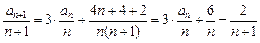 ∴
∴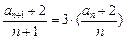
∴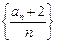 是首项为
是首项为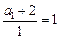 ,公比
,公比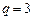 的等比数列…………4分
的等比数列…………4分
∴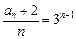 ∴
∴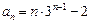
(2)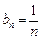 ,当
,当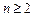 时,
时,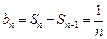 ,
,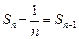 ………………5分
………………5分
两边平方得: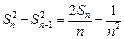
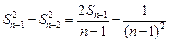
 ……
……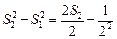
相加得: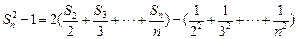
又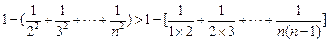
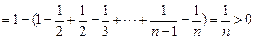 ∴
∴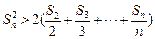 …………9分
…………9分
(3)(数学归纳法)当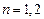 时,显然成立
时,显然成立
当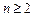 时,证明加强的不等式
时,证明加强的不等式
假设当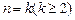 时命题成立,即
时命题成立,即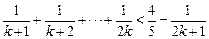
则当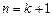 时
时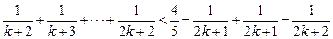
 ∴当
∴当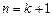 时命题成立,故原不等式成立…14
时命题成立,故原不等式成立…14
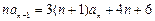 ,两边同除以
,两边同除以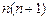 得:
得: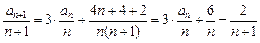 ∴
∴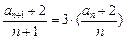
∴
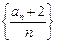 是首项为
是首项为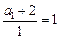 ,公比
,公比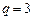 的等比数列…………4分
的等比数列…………4分∴
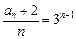 ∴
∴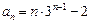
(2)
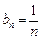 ,当
,当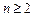 时,
时,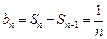 ,
,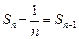 ………………5分
………………5分两边平方得:
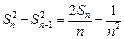
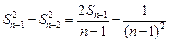
 ……
……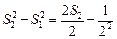
相加得:
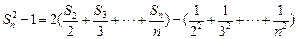
又
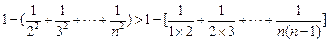
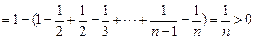 ∴
∴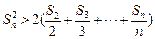 …………9分
…………9分(3)(数学归纳法)当
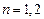 时,显然成立
时,显然成立当
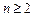 时,证明加强的不等式
时,证明加强的不等式
假设当
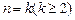 时命题成立,即
时命题成立,即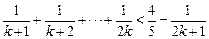
则当
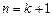 时
时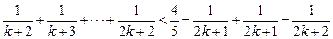
 ∴当
∴当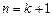 时命题成立,故原不等式成立…14
时命题成立,故原不等式成立…14
练习册系列答案
相关题目
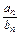 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.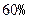 (即衰变了
(即衰变了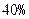 ),该动物大约在距今多少年前死亡?
),该动物大约在距今多少年前死亡?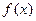 满足下列条件:
满足下列条件: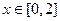 ,总有
,总有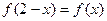 ,且
,且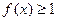 ,
,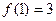 ;
;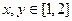 ,若
,若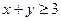 ,则
,则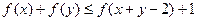 .
.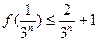 (
(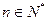 );(2)
);(2)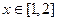 时,
时,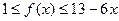 .
.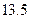 万元的新车,专家预测这种车每年按
万元的新车,专家预测这种车每年按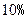 的速度折旧.
的速度折旧.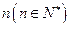 年后这辆车的价值.
年后这辆车的价值.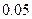 mm的报纸对折,再对折,再对折
mm的报纸对折,再对折,再对折 对折50次后,报纸的厚度是多少?你相信这时报纸的厚度可以在地球和月球之间建一座桥吗?
对折50次后,报纸的厚度是多少?你相信这时报纸的厚度可以在地球和月球之间建一座桥吗?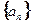 的前
的前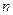 项和为
项和为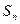 ,
,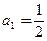 ,且
,且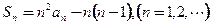
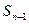 的递推关系式(
的递推关系式(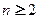 );
);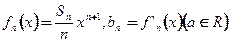 ,求数列
,求数列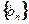 的前
的前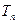 。
。