题目内容
已知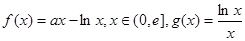 ,其中
,其中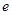 是自然常数,
是自然常数,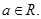
(Ⅰ)当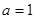 时, 研究
时, 研究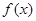 的单调性与极值;
的单调性与极值;
(Ⅱ)在(Ⅰ)的条件下,求证: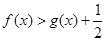 ;
;
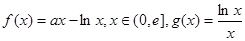 ,其中
,其中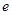 是自然常数,
是自然常数,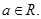
(Ⅰ)当
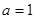 时, 研究
时, 研究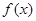 的单调性与极值;
的单调性与极值; (Ⅱ)在(Ⅰ)的条件下,求证:
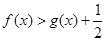 ;
;(Ⅰ)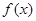 的极小值为
的极小值为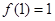 ;(Ⅱ)
;(Ⅱ)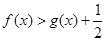 。
。
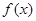 的极小值为
的极小值为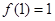 ;(Ⅱ)
;(Ⅱ)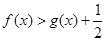 。
。试题分析:(1)因为
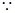
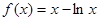 ,
,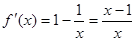 ,那么求解导数的正负,得到单调性的求解。
,那么求解导数的正负,得到单调性的求解。(2)
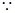
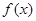 的极小值为1,即
的极小值为1,即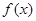 在
在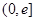 上的最小值为1,
上的最小值为1,∴
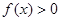 ,
,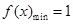 ,构造函数令
,构造函数令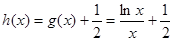 ,确定出最大值。比较大小得到。
,确定出最大值。比较大小得到。 解:(Ⅰ)
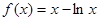 ,
,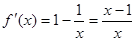 ……2分
……2分∴当
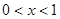 时,
时,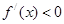 ,此时
,此时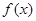 单调递减
单调递减当
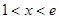 时,
时,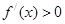 ,此时
,此时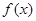 单调递增 …………4分
单调递增 …………4分 ∴
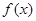 的极小值为
的极小值为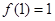 ……6分
……6分(Ⅱ)
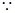
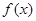 的极小值为1,即
的极小值为1,即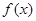 在
在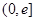 上的最小值为1,
上的最小值为1,∴
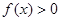 ,
,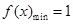 ……5分
……5分令
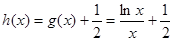 ,
,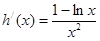 , …………8分
, …………8分 当
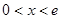 时,
时,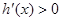 ,
,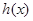 在
在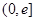 上单调递增 ………9分
上单调递增 ………9分∴
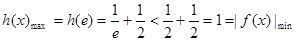 ………11分
………11分∴在(1)的条件下,
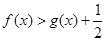 ……………………………12分
……………………………12分点评:解决该试题的关键是利用导数的正负判定函数单调性,和导数为零点的左右符号的正负,进而得到函数极值,进而求解最值。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
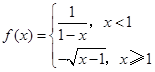 ,
,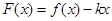 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性. 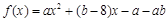
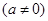 ,当
,当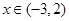 时,
时,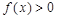 ;当
;当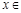 (
(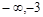 )
)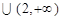 时,
时,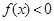 .
.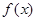 在[0,1]内的值域;
在[0,1]内的值域;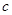 为何值时,不等式
为何值时,不等式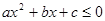 在[1,4]上恒成立.
在[1,4]上恒成立.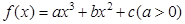 导函数图像的顶点坐标为
导函数图像的顶点坐标为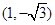 ,那么曲线
,那么曲线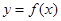 上任一点的切线的倾斜角
上任一点的切线的倾斜角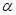 的取值范围是( )
的取值范围是( )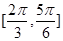
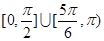
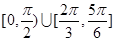
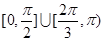
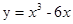 的极大值为( )
的极大值为( )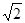
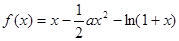 ,其中
,其中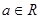 .
.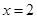 是
是 的极值点,求
的极值点,求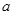 的值;
的值;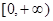 上的最大值是
上的最大值是 ,求
,求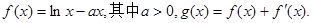
 的表达式;
的表达式;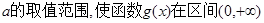 上是单调函数.
上是单调函数.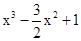 (2)
(2)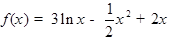
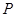 在曲线
在曲线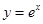 上,点
上,点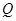 在曲线
在曲线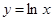 上,则
上,则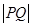 的最小值是
的最小值是