题目内容
(本小题共13分)设k∈R,函数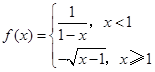 ,
,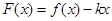 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性.
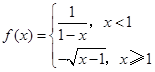 ,
,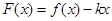 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性. 当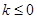 时,函数
时,函数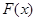 在
在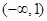 上是增函数;
上是增函数;
当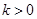 时,函数
时,函数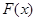 在
在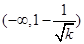 上是减函数,在
上是减函数,在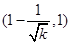 上是增函数;
上是增函数;
对于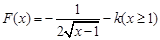 ,
,
当 时,函数
时,函数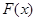 在
在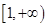 上是减函数;
上是减函数;
当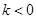 时,函数
时,函数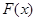 在
在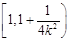 上是减函数,在
上是减函数,在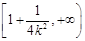 上是增函数。
上是增函数。
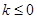 时,函数
时,函数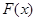 在
在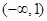 上是增函数;
上是增函数;当
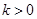 时,函数
时,函数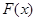 在
在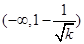 上是减函数,在
上是减函数,在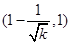 上是增函数;
上是增函数;对于
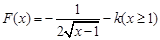 ,
,当
 时,函数
时,函数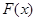 在
在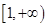 上是减函数;
上是减函数;当
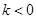 时,函数
时,函数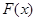 在
在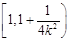 上是减函数,在
上是减函数,在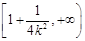 上是增函数。
上是增函数。试题分析:分段函数的单调性,导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,以及分类讨论的数学思想 来求解得到。
.解:
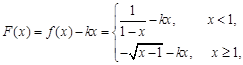 ,
, 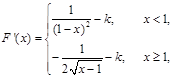
对于
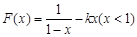 ,
,当
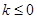 时,函数
时,函数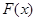 在
在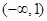 上是增函数;
上是增函数;当
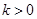 时,函数
时,函数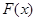 在
在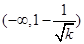 上是减函数,在
上是减函数,在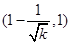 上是增函数;
上是增函数;对于
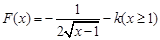 ,
,当
 时,函数
时,函数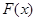 在
在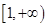 上是减函数;
上是减函数;当
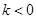 时,函数
时,函数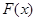 在
在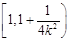 上是减函数,在
上是减函数,在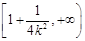 上是增函数。
上是增函数。点评:解决该试题的关键是先求出F(x)的解析式,然后求出导函数,讨论x与1的大小,然后分别讨论k与0的大小,根据导函数F′(x)的符号得到函数F(x)的单调区间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,曲线
,曲线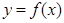 过点
过点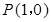 ,且在点
,且在点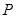 处的切线斜率为2.
处的切线斜率为2.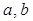 的值;
的值;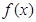 的极值点;
的极值点;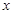 ,不等式
,不等式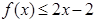 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。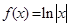
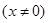 ,函数
,函数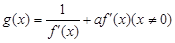
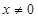 时,求函数
时,求函数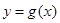 的表达式;
的表达式;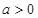 ,且函数
,且函数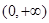 上的最小值是2 ,求
上的最小值是2 ,求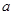 的值;
的值;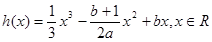 ,恰有三个零点,求b的取值范围。
,恰有三个零点,求b的取值范围。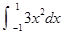 的值等于 .
的值等于 .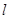 (单位:m)的乘积与车距d成正比,且最小车距不得少于半个车身长.假定车身长均为
(单位:m)的乘积与车距d成正比,且最小车距不得少于半个车身长.假定车身长均为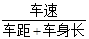 )
) 记
记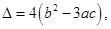 则当
则当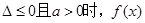 的大致图像为( )
的大致图像为( )
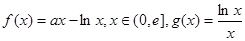 ,其中
,其中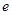 是自然常数,
是自然常数,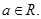
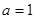 时, 研究
时, 研究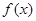 的单调性与极值;
的单调性与极值; 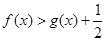 ;
;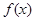 的图象如图所示,则不等式
的图象如图所示,则不等式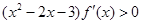 的解集为( )
的解集为( )