题目内容
已知:函数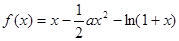 ,其中
,其中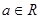 .
.
(Ⅰ)若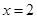 是
是 的极值点,求
的极值点,求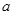 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在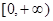 上的最大值是
上的最大值是 ,求
,求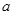 的取值范围.
的取值范围.
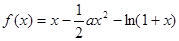 ,其中
,其中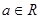 .
.(Ⅰ)若
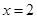 是
是 的极值点,求
的极值点,求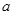 的值;
的值;(Ⅱ)求
 的单调区间;
的单调区间;(Ⅲ)若
 在
在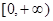 上的最大值是
上的最大值是 ,求
,求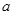 的取值范围.
的取值范围.(Ⅰ)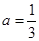
(Ⅱ)当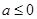 时,
时, 的增区间是
的增区间是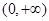 ,减区间是
,减区间是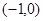 ;
;
当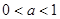 时,
时, 的增区间是
的增区间是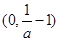 ,减区间是
,减区间是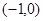 和
和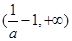 ;
;
当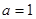 时,
时, 的减区间是
的减区间是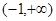 ;
;
当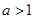 时,
时, 的增区间是
的增区间是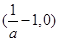 ;减区间是
;减区间是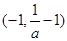 和
和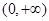 .
.
(Ⅲ)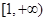
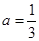
(Ⅱ)当
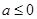 时,
时, 的增区间是
的增区间是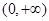 ,减区间是
,减区间是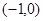 ;
;当
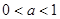 时,
时, 的增区间是
的增区间是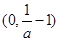 ,减区间是
,减区间是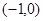 和
和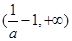 ;
;当
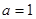 时,
时, 的减区间是
的减区间是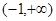 ;
;当
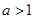 时,
时, 的增区间是
的增区间是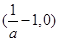 ;减区间是
;减区间是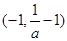 和
和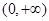 .
.(Ⅲ)
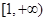
试题分析:(Ⅰ)
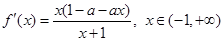 .
. 依题意,令
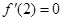 ,解得
,解得 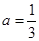 .
. 经检验,
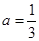 时,符合题意. ……4分
时,符合题意. ……4分 (Ⅱ)① 当
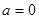 时,
时,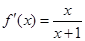 .
. 故
 的单调增区间是
的单调增区间是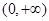 ;单调减区间是
;单调减区间是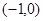 . ……5分
. ……5分② 当
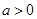 时,令
时,令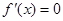 ,得
,得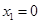 ,或
,或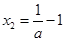 .
.当
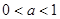 时,
时, 与
与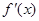 的情况如下:
的情况如下: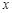 | 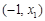 | 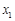 | 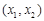 | 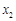 | 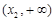 |
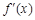 | 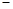 |  |  |  |  |
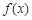 | ↘ | 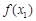 | ↗ | 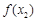 | ↘ |
 的单调增区间是
的单调增区间是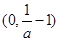 ;单调减区间是
;单调减区间是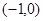 和
和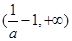 .
. 当
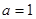 时,
时, 的单调减区间是
的单调减区间是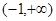 .
.当
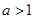 时,
时,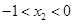 ,
, 与
与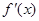 的情况如下:
的情况如下: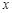 | 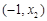 | 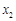 | 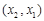 | 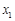 | 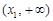 |
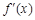 | 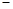 |  |  |  |  |
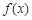 | ↘ | 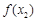 | ↗ | 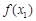 | ↘ |
 的单调增区间是
的单调增区间是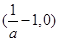 ;单调减区间是
;单调减区间是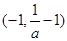 和
和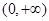 .
.③ 当
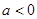 时,
时, 的单调增区间是
的单调增区间是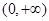 ;单调减区间是
;单调减区间是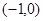 .
.综上,当
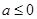 时,
时, 的增区间是
的增区间是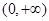 ,减区间是
,减区间是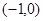 ;
;当
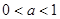 时,
时, 的增区间是
的增区间是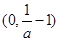 ,减区间是
,减区间是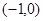 和
和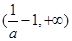 ;
;当
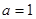 时,
时, 的减区间是
的减区间是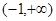 ;
;当
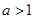 时,
时, 的增区间是
的增区间是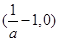 ;减区间是
;减区间是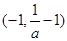 和
和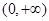 . ……11分
. ……11分(Ⅲ)由(Ⅱ)知
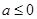 时,
时, 在
在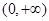 上单调递增,
上单调递增,由
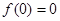 ,知不合题意.
,知不合题意.当
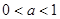 时,
时, 在
在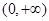 的最大值是
的最大值是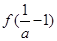 ,
,由
 ,知不合题意.
,知不合题意.当
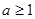 时,
时, 在
在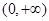 单调递减,
单调递减,可得
 在
在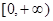 上的最大值是
上的最大值是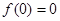 ,符合题意.
,符合题意. 所以,
 在
在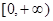 上的最大值是
上的最大值是 时,
时,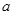 的取值范围是
的取值范围是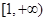 . ……14分
. ……14分点评:用导数求函数的单调区间时最好画出表格,这样既清楚又简单,另外分类讨论时要尽量做到不重不漏.

练习册系列答案
相关题目
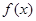 ,恒有
,恒有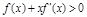 ,则
,则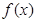 是最小正周期为
是最小正周期为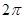 的偶函数,
的偶函数,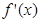 是
是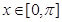 时,
时,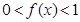 ;当
;当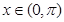 且
且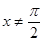 时,
时,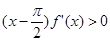 ,则函数
,则函数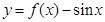 在
在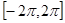 上的零点个数为
上的零点个数为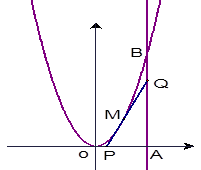
 记
记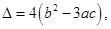 则当
则当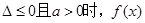 的大致图像为( )
的大致图像为( )
 .
.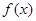 在
在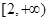 上是增函数,求实数
上是增函数,求实数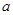 的取值范围;
的取值范围;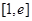 上的最小值为3,求实数
上的最小值为3,求实数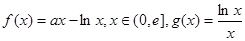 ,其中
,其中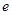 是自然常数,
是自然常数,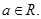
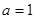 时, 研究
时, 研究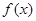 的单调性与极值;
的单调性与极值; 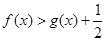 ;
;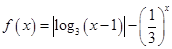 有两个零点
有两个零点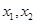 ,则( )
,则( )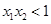
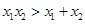
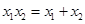
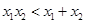
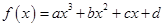 的图象(如图),则函数
的图象(如图),则函数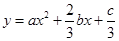 的单调递增区间是( )
的单调递增区间是( )