题目内容
设a>0,f(x)=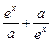 是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
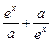 是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数. (1) a=1 (2) 证明略
依题意,对一切x∈R,有f(x)=f(-x),
即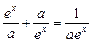 +aex
+aex 整理,得(a-
整理,得(a-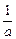 )(ex-
)(ex-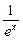 )=0.
)=0.
因此,有a-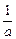 =0,即a2=1,又a>0,∴a=1.
=0,即a2=1,又a>0,∴a=1.
(2)证法一(定义法): 设0<x1<x2,
则f(x1)-f(x2)=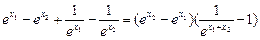
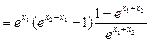
由x1>0,x2>0,x2>x1,∴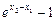 >0,1-e
>0,1-e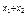 <0,
<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴f(x)在(0,+∞)上是增函数.
证法二(导数法): 由f(x)=ex+e-x,得f′(x)=ex-e-x=e-x·(e2x-1).当x∈(0,+∞)时,e-x>0,e2x-1>0.
此时f′(x)>0,所以f(x)在[0,+∞)上是增函数.
即
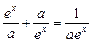 +aex
+aex 整理,得(a-
整理,得(a-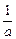 )(ex-
)(ex-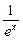 )=0.
)=0. 因此,有a-
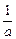 =0,即a2=1,又a>0,∴a=1.
=0,即a2=1,又a>0,∴a=1. (2)证法一(定义法): 设0<x1<x2,
则f(x1)-f(x2)=
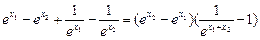
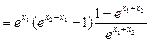
由x1>0,x2>0,x2>x1,∴
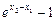 >0,1-e
>0,1-e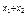 <0,
<0,∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴f(x)在(0,+∞)上是增函数.
证法二(导数法): 由f(x)=ex+e-x,得f′(x)=ex-e-x=e-x·(e2x-1).当x∈(0,+∞)时,e-x>0,e2x-1>0.
此时f′(x)>0,所以f(x)在[0,+∞)上是增函数.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
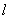 上,
上,
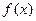 =
=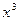 +a
+a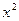 +b的图象在点P (1,0)处的切线与直线3x+y=0平行.则a、b的值分别为( ).
+b的图象在点P (1,0)处的切线与直线3x+y=0平行.则a、b的值分别为( ). =x.
=x. 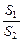 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域. 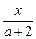 =|a-1|+2的根的取值范围.
=|a-1|+2的根的取值范围.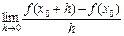
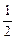 ,
,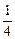 )的切线的倾斜角是
)的切线的倾斜角是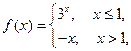 若
若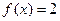 ,则
,则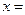 .
.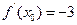 ,则
,则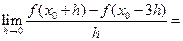 ( )
( )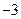 B
B 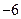
 D
D