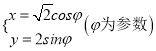题目内容
【题目】设函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间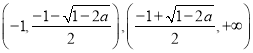 单调递增; 在区间
单调递增; 在区间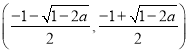 函数
函数![]() 单调递减;
单调递减;
当![]() 时,
时, 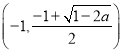 函数
函数![]() 单调递减,
单调递减, 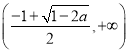 函数
函数![]() 单调递增;
单调递增;
(Ⅱ)见解析.
【解析】试题分析:
试题分析:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,得到
,得到![]() ,令
,令![]() ,则
,则![]() ,分
,分![]() 和
和![]() 分类讨论,即可求解函数的单调区间.
分类讨论,即可求解函数的单调区间.
(Ⅱ)当函数![]() 有两个极值点时,得
有两个极值点时,得![]() ,令
,令![]() ,利用
,利用![]() 和函数
和函数![]() 的最值,即可证明结论.
的最值,即可证明结论.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,
![]() 令
令![]() ,则
,则![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() ,从而
,从而![]() ,故函数
,故函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时, ![]() ,
, ![]() 的两个根为
的两个根为 ![]() ,
,
当![]() 时,
时, ![]() ,此时,当
,此时,当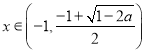 函数
函数![]() 单调递减;当
单调递减;当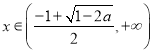 函数
函数![]() 单调递增.
单调递增.
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 在区间
在区间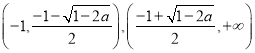 单调递增;当
单调递增;当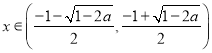 函数
函数![]() 单调递减.
单调递减.
综上: 当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间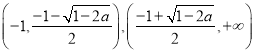 单调递增; 在区间
单调递增; 在区间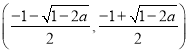 函数
函数![]() 单调递减; 当
单调递减; 当![]() 时,
时,  函数
函数![]() 单调递减,
单调递减, 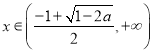 函数
函数![]() 单调递增.
单调递增.
(Ⅱ)当函数![]() 有两个极值点时,
有两个极值点时, ![]() ,
,![]() ,
,
且![]() 即
即![]() ,
,
![]()
![]()
![]()
![]()
令![]()
![]()
![]() ,令
,令![]() ,函数单调递增;
,函数单调递增;
令![]() ,函数单调递减;
,函数单调递减;
![]()
![]() ,
,![]()
![]()

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目