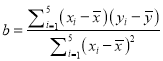题目内容
【题目】已知函数![]() 且
且![]() .
.
(I)若![]() ,求函数
,求函数![]() 的单调区间;(其中
的单调区间;(其中![]() 是自然对数的底数)
是自然对数的底数)
(II)设函数![]() ,当
,当![]() 时,曲线
时,曲线![]() 与
与![]() 有两个交点,求
有两个交点,求![]() 的取值范围.
的取值范围.
【答案】(I)增区间为![]() ,减区间为
,减区间为![]() (II)
(II)![]()
【解析】试题分析:(I)定义域![]() ,求得
,求得![]() 利用
利用![]() ,
, ![]() ,即可判定函数的单调区间;
,即可判定函数的单调区间;
(II)联立两函数得![]() ,令
,令![]()
可得![]() ,根据
,根据![]() 和
和![]() 分类讨论,即可求
分类讨论,即可求![]() 的取值范围。
的取值范围。
试题解析:
(I)定义域![]()
![]() 时,
时, ![]()
由![]() 得
得![]() 增区间为
增区间为![]() ,
,
由![]() 得
得![]() 减区间为
减区间为![]()
(II)联立![]() 与
与![]() 得
得![]() =
=![]() ,
, ![]()
令![]()
![]()
则![]()
当![]() 时,
时, ![]() ,
,
由![]() 得,
得, ![]() ,
, ![]() 在
在![]() 上单调递增
上单调递增
由![]() 得,
得, ![]() ,
, ![]() 在
在![]() 上单调递减
上单调递减
![]()
由题意得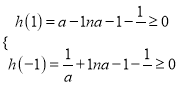
令![]() ,则
,则![]() ,
,
![]() 单调递增,
单调递增, ![]()
![]()
令![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ,
, ![]() 合题意
合题意
当![]() 时,
时, ![]() ,
,
由![]() 得,
得, ![]() ,/span>
,/span> ![]() 在
在![]() 上单调递增
上单调递增
由![]() 得,
得, ![]() ,
, ![]() 在
在![]() 上单调递减
上单调递减
![]()
由题意得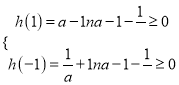
令![]() 单调递减,
单调递减,
![]()
![]()
令![]() ,则
,则![]() ,
,
![]() 单调递减
单调递减
![]() 时,
时, ![]()
![]()
![]() 合题意.
合题意.
综上, ![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() ,试求出
,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.