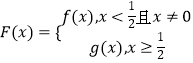题目内容
【题目】设函数
，若过点
可作三条直线与曲线
相切，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】f(x)=x33x2,则f′(x)=3x26x，
设切点为(x0,x303x20),则f′(x0)=3x206x0.
∴过切点处的切线方程为yx30+3x20=(3x206x0)(xx0)，
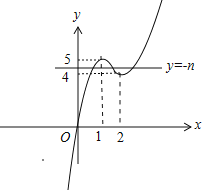
把点(2,n)代入得：nx30+3x20=(3x206x0)(2x0).
整理得：2x309x20+12x0+n=0.
若过点(2,n)可作三条直线与曲线y=f(x)相切,则方程2x309x20+12x0+n=0有三个不同根
令g(x)=2x39x2+12x，
则g′(x)=6x218x+12=6(x1)(x2)，
∴当x∈(∞,1)∪(2,+∞)时,g′(x)>0;当x∈(1,2)时,g′(x)<0，
∴g(x)的单调增区间为(∞,1),(2,+∞);单调减区间为(1,2).
∴当x=1时,g(x)有极大值为g(1)=5;当x=2时,g(x)有极小值为g(2)=4.
由4<n<5，得5<n<4.
∴实数n的取值范围是(5,4).
故选：A.
练习册系列答案
相关题目
