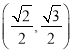题目内容
【题目】已知长方形![]() ,
, ![]() ,
, ![]() ,以
,以![]() 的中点
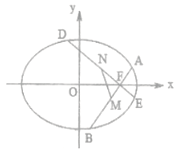
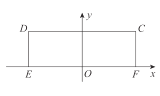
的中点![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系![]() .
.
(1)求以![]() 为焦点,且过
为焦点,且过![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点![]() 作直线
作直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,设
,设![]() ,点
,点![]() 坐标为
坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)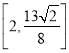 .
.
【解析】试题分析:(1)确定![]() 的坐标,利用椭圆的定义,求出几何量,即可求椭圆的标准方程;(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求
的坐标,利用椭圆的定义,求出几何量,即可求椭圆的标准方程;(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求![]() 的取值范围.
的取值范围.
试题解析:(1)由题意可得点![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,
, 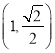 .设椭圆的标准方程是
.设椭圆的标准方程是![]() ,则
,则![]() ,∴
,∴![]() .∴
.∴![]() ,∴椭圆的标准方程为
,∴椭圆的标准方程为![]() .
.
(2)由题意容易验证直线![]() 的斜率不为0,故可设直线
的斜率不为0,故可设直线![]() 的方程为
的方程为![]() .代入
.代入![]() 中,得
中,得![]() .设
.设![]() ,
, ![]() ,由根与系数关系,得
,由根与系数关系,得![]() ①,
①,![]() ②,∵
②,∵![]() ,∴
,∴![]() 且
且![]() ,将上式①的平方除以②,得
,将上式①的平方除以②,得![]() ,即
,即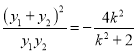 ,所以
,所以![]() ,由
,由![]()
![]() ,即
,即![]() .∵
.∵![]() ,
, ![]() ,
, ![]() ,又
,又![]() ,
, ![]() .故
.故![]()
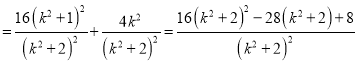
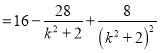 .令
.令![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,
, 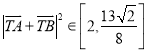 .
.

 高中必刷题系列答案
高中必刷题系列答案【题目】设全集U={(x,y)|x,y∈R},集合M={(x,y)| ![]() =1},N={(x,y)|y=x+1},则N∩(UM)等于( )
=1},N={(x,y)|y=x+1},则N∩(UM)等于( )
A.
B.{(2,3)}
C.(2,3)
D.{(x,y)|y=x+1}
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() ,试求出
,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:

(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注:![]()