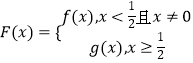Question

【题目】已知函数（）的图象与直线相切，当恰有一个零点时，实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】由题意,取切点(m,n),则,m=2n,

∴a=e.∴，

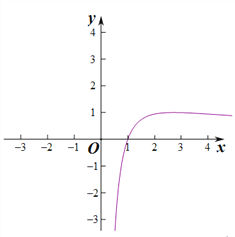
,函数f(x)在(0,e)上单调递增,(e,+∞)上单调递减，

f(1)=0,x→+∞,f(x)→0，

由于f(e)=1,f(1)=0，

∴当函数g(x)=f(f(x))t恰有一个零点时,实数t的取值范围是{0}，

故选A.

点睛:已知函数有零点求参数常用的方法和思路：

直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；

分离参数法：先将参数分离，转化成函数的值域问题解决；

数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.