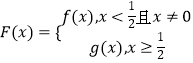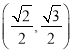题目内容
【题目】已知函数f(x)=x+ ![]() ,且函数y=f(x)的图像经过点(1,2).
,且函数y=f(x)的图像经过点(1,2).
(1)求m的值;
(2)判断函数的奇偶性并加以证明;
(3)证明:函数f(x)在(1,+∞)上是增函数.
【答案】
(1)解:由函数f(x)=x+ ![]() 的图像过点(1,2),
的图像过点(1,2),
得2=1+ ![]() ,
,
解得m=1
(2)解:由(1)知,f(x)=x+ ![]() ,
,
定义域为(﹣∞,0)∪(0,+∞)具有对称性,
且f(﹣x)=﹣x+ ![]() =﹣(x+
=﹣(x+ ![]() )=﹣f(x),
)=﹣f(x),
所以f(x)为奇函数
(3)证明:设1<x1<x2,则
f(x1)﹣f(x2)= ![]() =
= ![]() ,
,
∵x1﹣x2<0,x1x2﹣1>0,x1x2>0,
∴f(x1)<f(x2),
∴函数y=f(x)在(1,+∞)上为增函数
【解析】(1)由函数f(x)图像过点(1,2),代入解析式求出m的值;(2)利用奇偶性的定义判断f(x)为定义域上的奇函数;(3)利用单调性的定义可证明f(x)在(1,+∞)上为增函数.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.

【题目】设全集U={(x,y)|x,y∈R},集合M={(x,y)| ![]() =1},N={(x,y)|y=x+1},则N∩(UM)等于( )
=1},N={(x,y)|y=x+1},则N∩(UM)等于( )
A.
B.{(2,3)}
C.(2,3)
D.{(x,y)|y=x+1}
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() ,试求出
,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】甲、乙两种不同规格的产品,其质量按测试指标分数进行划分,其中分数不小于82分的为合格品,否则为次品.现随机抽取两种产品各100件进行检测,其结果如下:
测试指标分数 |
|
|
|
|
|
甲产品 | 8 | 12 | 40 | 32 | 8 |
乙产品 | 7 | 18 | 40 | 29 | 6 |
(1)根据以上数据,完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的有把握认为两种产品的质量有明显差异?
的有把握认为两种产品的质量有明显差异?
甲产品 | 乙产品 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(2)已知生产1件甲产品,若为合格品,则可盈利40元,若为次品,则亏损5元;生产1件乙产品,若为合格品,则可盈利50元,若为次品,则亏损10元.记![]() 为生产1件甲产品和1件乙产品所得的总利润,求随机变量
为生产1件甲产品和1件乙产品所得的总利润,求随机变量![]() 的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |