题目内容
已知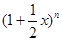 展开式的各项依次记为
展开式的各项依次记为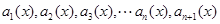 .
.
设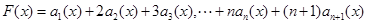 .
.
(1)若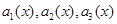 的系数依次成等差数列,求
的系数依次成等差数列,求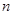 的值;
的值;
(2)求证:对任意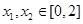 ,恒有
,恒有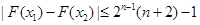 .
.
(1)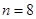 (2)不等式的恒成立
(2)不等式的恒成立
解析试题分析:解:(1)依题意 ,
,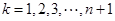 ,
,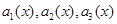 的系数依次为
的系数依次为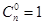 ,
,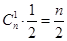 ,
,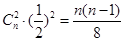 ,
,
所以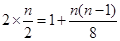 ,解得
,解得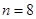 ; 4分
; 4分
(2)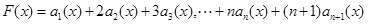
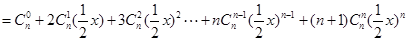
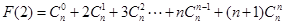
设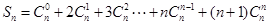 ,
,
则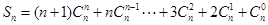
考虑到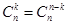 ,将以上两式相加得:
,将以上两式相加得:
所以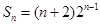
又当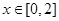 时,
时,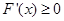 恒成立,从而
恒成立,从而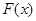 是
是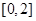 上的单调递增函数,
上的单调递增函数,
所以对任意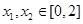 ,
,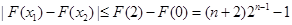 . 10分
. 10分
考点:二项式定理和导数的运用
点评:解决的关键是利用二项式定理以及导数的思想来证明不等式的成立,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

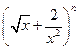 的展开式中,第3项的系数与倒数第3项的系数之比为
的展开式中,第3项的系数与倒数第3项的系数之比为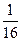 .
.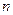 的值;
的值;