题目内容
【题目】已知函数![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称,且
对称,且![]() ,函数
,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上是单调递增函数,求实数
上是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的最大值为2,求实数
的最大值为2,求实数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据反函数的概念求得![]() 解析式,利用
解析式,利用![]() 列方程求得
列方程求得![]() 的值.
的值.
(2)利用二次函数的性质,结合复合函数单调性同增异减列不等式,解不等式求得实数![]() 的取值范围.
的取值范围.
(3)根据二次函数的性质,结合函数![]() 的最大值为
的最大值为![]() 列方程,解方程求得求实数
列方程,解方程求得求实数![]() 的值.
的值.
(1)由于函数![]() 的图像与
的图像与![]() 的图像关于
的图像关于![]() 对称,即函数
对称,即函数![]() 与
与![]() 互为反函数,故
互为反函数,故![]() .由
.由![]() ,所以
,所以![]() .
.
(2)由(1)知![]() ,所以
,所以![]()
![]() .当
.当![]() 时,
时,![]() ,要使函数
,要使函数![]() 在
在![]() 上是单调递增函数,结合二次函数的性质结合复合函数单调性同增异减可知,
上是单调递增函数,结合二次函数的性质结合复合函数单调性同增异减可知,![]() .
.
(3)由(2)得![]() .当
.当![]() 时,
时,![]() .所以
.所以
当![]() 时,
时,![]() ,不符合.
,不符合.
当![]() 时,
时,![]() ,符合.
,符合.
当![]() 时,
时,![]() ,不符合.
,不符合.
综上所述,实数![]() 的值为
的值为![]() .
.

【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制,已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
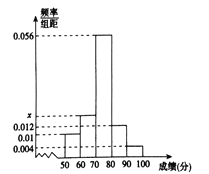
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若该校高三学生共1000人,求竞赛等级在良好及良好以上的人数;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取2名学生进行学习经验介绍,求抽取的2名学生中优秀等级的学生恰好有1人的概率.