Question

【题目】已知数集具有性质：对任意的、，与两数中至少有一个属于.

（1）分别判断数集与是否具有性质，并说明理由；

（2）证明：且；

（3）证明：当时，.

Answer 1

【答案】（1）不具有性质，具有性质，理由详见解析；（2）证明见解析；（3）证明见解析.

【解析】

（1）由定义直接判断集合和是否具有性质；

（2）由已知得和中至少有一个属于，从而得到，再由，得到，由具有性质可知，由此能证明；

（3）当时，，从而，，由此能证明.

（1）由于和均不属于数集，所以，数集不具有性质.

由于、、、、、、、、、都属于数集，所以，数集具有性质；

（2）数集具有性质，

所以，和中至少有一个属于，，所以，则，从而，故.

，所以，，故.

因为，数集具有性质可知，.

又因为，，，，，.

所以，.

因此，；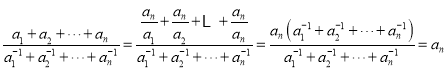

（3）由（2）知，，，即，

因为，所以，，则，由于数集具有性质，.

由，可得，且，所以，，

故，因此，.