题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 上的动点
上的动点![]() 到两焦点的距离之和为4,当点
到两焦点的距离之和为4,当点![]() 运动到椭圆
运动到椭圆![]() 的上顶点时,直线
的上顶点时,直线![]() 恰与以原点
恰与以原点![]() 为圆心,以椭圆
为圆心,以椭圆![]() 的离心率为半径的圆相切.
的离心率为半径的圆相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,若
,若![]() 交直线
交直线![]() 于
于![]() 两点.问以
两点.问以![]() 为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]()
【解析】试题分析:(1)由椭圆定义可知![]() ,
,![]() ,由原点到直线
,由原点到直线![]() 的距离求出
的距离求出![]() ,得到椭圆的标准方程;(2)设
,得到椭圆的标准方程;(2)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,求出M,N的坐标,因为
,求出M,N的坐标,因为![]() ,故以
,故以![]() 为直径的圆与
为直径的圆与![]() 轴交于两点,在以
轴交于两点,在以![]() 为直径的圆中应用相交弦定理求出
为直径的圆中应用相交弦定理求出![]() ,从而以
,从而以![]() 为直径的圆恒过两个定点
为直径的圆恒过两个定点![]() ,
,![]() .
.
试题解析:(1)由椭圆定义可知![]() ,
,![]() ,
,
直线![]() ,
,
故![]() ,
,
∴![]() ,
,
故椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
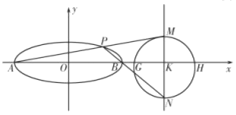
(2)设![]() ,点
,点![]() ,则
,则![]() ,
,![]() ,
,
由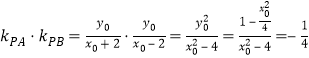 ,得:
,得:![]() ,
,
直线![]() 方程为:
方程为:![]() ,令
,令![]() ,则
,则![]() ,故
,故![]() ;
;
直线![]() 方程为:
方程为:![]() ,令
,令![]() ,则
,则![]() ,故
,故![]() ;
;
因为![]() ,故以
,故以![]() 为直径的圆与
为直径的圆与![]() 轴交于两点,设为
轴交于两点,设为![]() ,
,
在以![]() 为直径的圆中应用相交弦定理得:
为直径的圆中应用相交弦定理得:
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
从而以![]() 为直径的圆恒过两个定点
为直径的圆恒过两个定点![]() ,
,![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.