题目内容
9.函数f(x)=9-8cosx-2sin2x的最大值是17.分析 由条件利用同角三角函数的基本关系化简函数的解析式,再利用二次函数的性质求得f(x)的最大值.
解答 解:函数f(x)=9-8cosx-2sin2x=2cos2x-8cosx+7=2(cosx-2)2-1,
故当cosx=-1时,函数f(x)取得最大值为17,
故答案为:17.
点评 本题主要考查同角三角函数的基本关系,二次函数的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则目标函数z=$\frac{y+1}{x+1}$的最大值为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{6}{5}$ | D. | $\frac{2}{3}$ |
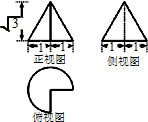 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{\sqrt{3}π}{4}$;表面积为$\frac{9π}{4}+\sqrt{3}$.